L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
En triplant les longueurs des côtés d'un triangle, comment les mesures des angles sont-elles modifiées ?
Elles sont multipliées par 3.
Elles sont divisées par 3.
Elles sont multipliées par 9.
Elles sont conservées.
Essayez de vous représenter la situation dans la tête.
Le triangle de départ, et à côté, le triangle agrandi.
Question 2
En triplant les longueurs des côtés d'un triangle, comment l'aire du triangle est-elle modifiée ?
Elle est multipliée par 3.
Elle est divisée par 3.
Elle est multipliée par 9.
Elle est conservée.
Lorsque les dimensions d’une figure sont multipliées par k, son aire est multipliée par k2.
Question 3
En doublant les longueurs des arêtes d'un cube, comment l'aire de chaque face du cube est-elle modifiée ?
Elle est multipliée par 2.
Elle est divisée par 2.
Elle est multipliée par 4.
Elle est conservée.
Lorsque les dimensions d’une figure sont multipliées par k, son aire est multipliée par k2.
Question 4
En doublant les longueurs des arêtes d'un cube, comment le volume du cube est-il modifié ?
Il est multiplié par 2.
Il est multiplié par 4.
Il est multiplié par 6.
Il est multiplié par 8.
Lorsque les dimensions d’une figure sont multipliées par k, son aire est multipliée par k2.
Question 5
Les dimensions d'une figure sont multipliées par un nombre k. Il s'agit d'une réduction ou d'un agrandissement ?
C’est une réduction.
C’est un agrandissement.
Ça dépend du signe de k.
k est positif. Ça dépend s’il est plus petit ou plus grand que 1.
k ne peut pas être négatif, car cela nous donnerait des longueurs négatives, ce qui est impossible.
Multiplier une longueur par un nombre supérieur à 1 « agrandit » cette longueur.
Multiplier une longueur par un nombre compris entre 0 et 1 « diminue » cette longueur.
Question 6
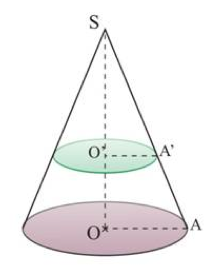
On considère les cônes ci-dessous :
- Le grand cône de sommet \(S\) et de base le disque de centre \(O\) et de rayon \(OA\).
- Le petit cône de sommet \(S\) et de base le disque de centre \(O\) et de rayon \(OA\).
\(SO = 12\) cm ; \(SO = 8\) cm et \(SA = 15\) cm
À combien est égal k, le coefficient de réduction ?
\(k = \dfrac{SO}{SO'} = \dfrac{12}{8} = \dfrac{3}{2} = 15\)
\(k = \dfrac{SA}{SO} = \dfrac{15}{12} = \dfrac{5}{4} = 1,25\)
\(k = \dfrac{SO'}{SO} = \dfrac{8}{12} = \dfrac{2}{3} \approx 0,67\)
\(k = \dfrac{SO}{SA} = \dfrac{12}{15} = \dfrac{4}{5} = 0,8\)
Puisque qu’il s’agit d’une réduction, le nombre k doit être compris entre 0 et 1.
Trouvez une longueur sur le grand cône puis sa longueur « associée » sur le petit cône.
Question 7
On considère les cônes ci-dessous :
- Le grand cône de sommet \(S\) et de base le disque de centre \(O\) et de rayon \(OA\).
- Le petit cône de sommet \(S\) et de base le disque de centre \(O'\) et de rayon \(OA\).
\(SO = 12\) cm ; \(SO = 8\) cm et \(SA = 15\) cm

Quel rapide calcul permet de déterminer la longueur \(OA\) ?
\(OA = SA - SO = 15 - 12 = 3 \)
\(OA^2 = SA^2 - SO^2 = 15^2 - 12^2 = 225 - 144 = 81 \)
Donc \(OA = 40,5\)
\(OA^2 = SA^2 + SO^2 = 15^2 + 12^2 = 225 + 144 = 369 \)
Donc \(OA = 19,2\)
\(OA^2 = SA^2 - SO^2 = 15^2 - 12^2 = 225 - 144 = 81 \)
Donc \(OA = 9\)
Le triangle \(SOA\) est un triangle rectangle en \(O\).
Pensez au théorème de Pythagore bien sûr.
Question 8
On considère les cônes ci-dessous :
- Le grand cône de sommet \(S\) et de base le disque de centre \(O\) et de rayon \(OA\).
- Le petit cône de sommet \(S\) et de base le disque de centre \(O\) et de rayon \(OA\).
\(SO = 12\) cm ; \(SO = 8\) cm et \(SA = 15\) cm

Sachant que \(OA^2 =9\), quelle est la valeur exacte de l'aire du disque de base du grand cône ?
\(Aire = \pi \times R^2 = \pi \times 9^2 = 81 \pi\)
\(Aire = 2 \times \pi \times R^2 = 2 \times \pi \times 9^2 = 162 \pi\)
\(Aire = 2 \times \pi \times R = 2 \times \pi \times 9 = 18 \pi\)
\(Aire = \pi \times R = \pi \times 9 = 81 \pi\)
Aire d’un disque de rayon \(R = \pi \times R^2\)
Question 9
On considère les cônes ci-dessous :
- Le grand cône de sommet \(S\) et de base le disque de centre \(O\) et de rayon \(OA\).
- Le petit cône de sommet \(S\) et de base le disque de centre \(O\) et de rayon \(OA\).
\(SO = 12\) cm ; \(SO = 8\) cm et \(SA = 15\) cm

L'aire du disque de base du grand cône est de \(81\pi\).
En utilisant \(k = \dfrac{2}{3}\), le rapport de réduction, quelle est la valeur exacte de l'aire du disque de base du petit cône ?
Aire du petit cône :
= Aire du grand cône \(\times \dfrac{2}{3} = 81\pi \times \dfrac{2}{3} = 54 \pi\) cm2
Aire du petit cône :
= Aire du grand cône \( \times \left(\dfrac{2}{3}\right)^2\)= \(81 \pi \times \left(\dfrac{2}{3}\right)^2\)= \(81\pi \times \dfrac{4}{9} = 36 \pi\) cm2
Aire du petit cône :
= Aire du grand cône \( \times \left(\dfrac{2}{3}\right)^2\)= \(81 \pi \times \left(\dfrac{2}{3}\right)^2\)= \(81\pi \times \dfrac{8}{27} = 24 \pi\) cm2
Aire du petit cône :
= Aire du grand cône \(\times \dfrac{2}{3} = 81\pi \times \dfrac{2}{3} = 121,5\pi\) cm2
Lorsque les dimensions d’une figure sont multipliées par k, son aire est multipliée par k2.
Question 10
On considère les cônes ci-dessous :
- Le grand cône de sommet S et de base le disque de centre O et de rayon \(OA\).
- Le petit cône de sommet S et de base le disque de centre O et de rayon \(OA\).
\(SO = 12\) cm ; \(SO = 8\) cm et \(SA = 15\) cm

Quelle est la valeur exacte du volume du grand cône ?
Volume :
= Aire de la base \(\times\) hauteur \(= 81 \pi \times 12 = 972 \pi\) cm3
Volume :
\(= \dfrac{4}{3} \times \) Aire de la base \(\times\) hauteur \(= \dfrac{4}{3} \times 81\pi \times 12 = 1296 \pi\) cm3
Volume :
\(= \dfrac{1}{3} \times \) Aire de la base \(\times\) hauteur \(= \dfrac{1}{3} \times 81\pi \times 12 = 324 \pi\) cm3
Aucune des réponses précédentes n’est exacte.
Formule à savoir par cœur : Volume du cône \(= \dfrac{1}{3} \times \) Aire de la base \(\times\) hauteur.
Question 11
On considère les cônes ci-dessous :
- Le grand cône de sommet S et de base le disque de centre O et de rayon \(OA\).
- Le petit cône de sommet S et de base le disque de centre O et de rayon \(OA\).
\(SO = 12\) cm ; \(SO = 8\) cm et \(SA = 15\) cm

Le volume du grand cône est de \(324 \pi\) cm3.
En utilisant \(k =\dfrac{2}{3}\) le rapport de réduction, quelle est la valeur exacte du volume du petit cône ?
Volume du petit cône :
= Volume du grand cône \( \times \dfrac{2}{3} = 324\pi \times\dfrac{2}{3} = 216 \pi \) cm3
Volume du petit cône :
= Volume du grand cône \( \times \left(\dfrac{2}{3}\right)^2\)\(= 324\pi \times\dfrac{4}{9} = 144 \pi \) cm3
Volume du petit cône :
= Volume du grand cône \( \times \left(\dfrac{2}{3}\right)^3\)\(= 324\pi \times\dfrac{8}{27} = 96 \pi \) cm3
Aucune des réponses précédentes n’est exacte.
Lorsque les dimensions d’une figure sont multipliées par k, son volume est multiplié par k3.
