L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
Tu as obtenu le score de
Question 1
Nous voici dans une situation de Thalès :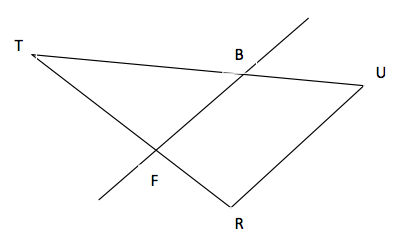
\(BU\) et \(FR\) se coupent en \(T\).
\((BF\)) et \((RU\)) sont parallèles.
\(TU = 5\) cm.
\(TB = 4\) cm et \(TF = 3\) cm.
On recherche la longueur \(TR\).
En appliquant le théorème de Thalès, quelle égalité obtient-on ?
\(\dfrac{TF}{TR} = \dfrac{TB}{TU} = \dfrac{FB}{RU} \)
\(\dfrac{TF}{FR} = \dfrac{TB}{BU} = \dfrac{FB}{RU} \)
\(\dfrac{RF}{RT} = \dfrac{UB}{UT} = \dfrac{FB}{RU} \)
\(\dfrac{TF}{TR} = \dfrac{TB}{TU} = \dfrac{RU}{FB} \)
Dans une situation de Thalès, un seul point n’appartient pas aux deux droites parallèles. On l’appelle parfois le « point-charnière ».
Ici, c’est le \(T\) qui joue ce rôle. Il intervient dans les numérateurs et les dénominateurs des deux premiers quotients que vous recherchez.
\(\dfrac{T...}{T...} = \dfrac{T...}{T...} = \dfrac{...}{...} \)
Question 2
\(BU\) et \(FR\) se coupent en \(T\).
\((BF\)) et \((RU\)) sont parallèles.
\(TU = 5\) cm.
\(TB = 4\) cm et \(TF = 3\) cm.
On sait que \(\dfrac{TF}{TR} = \dfrac{TB}{TU} = \dfrac{FB}{RU} \).
Si on remplace par les valeurs que l'on connait on obtient : \(\dfrac{3}{TR} = \dfrac{4}{5} = \dfrac{FB}{RU} \).
L'égalité des produits en croix appliquées aux deux premiers quotients nous donne :
\(3 \times TR = 4 \times 5\)
\(4 \times TR = 3 \times 5\)
\(5 \times TR = 3 \times 4\)
\(TR = 3 \times4 \times 5\)
Lorsque \(\dfrac{a}{b} = \dfrac{c}{d}\) alors \(a \times d = b \times c\).
Question 3
Puisque \(4 \times TR = 3 \times 5\), que vaut \(TR\) ?
\(TR = \dfrac{3 \times 4}{5} = 2,4\)
\(TR = \dfrac{3 \times 5}{4} = 3,75\)
\(TR = \dfrac{4 \times 5}{3} \approx 6,67\)
\(TR = 3 \times4 \times 5 = 60\)
Divise chaque membre par 4 afin d’isoler \(TR\).
Question 4
On se place à l'extérieur de la pyramide grise et on plante verticalement un bâton représenté par le segment \([BN]\) de \(2\) m de façon à ce que les points \(T, N, S\) et \(T, B, H \) soient alignés dans cet ordre.
On mesure que \(TB = 2,4\) m et \(TH = 165\) m.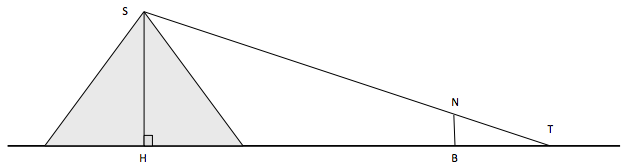
Pourquoi \((NB)\) et \((SH)\) sont parallèles ?
Parce que \(SHBN\) est un trapèze.
Parce qu’on peut utiliser la réciproque du théorème de Thalès.
Parce que \((SH)\) et \((NB)\) sont toutes les deux perpendiculaires à la même droite : \((BH)\).
Parce que \(SHBN\) est un parallélogramme.
C’est une règle de la classe de 6ème, bien utile pour prouver le parallélisme de deux droites.
Question 5
En appliquant le théorème de Thalès, quelle égalité obtient-on ?
\(\dfrac{TB}{TH} = \dfrac{TS}{TN} = \dfrac{BN}{HS}\)
\(\dfrac{TB}{TH} = \dfrac{TN}{TS} = \dfrac{SH}{NB}\)
\(\dfrac{HB}{HT} = \dfrac{SN}{ST} = \dfrac{SH}{NB}\)
\(\dfrac{TN}{TS} = \dfrac{TB}{TH} = \dfrac{NB}{SH}\)
Dans une situation de Thalès, un seul point n’appartient pas aux deux droites parallèles. On l’appelle parfois le « point-charnière ».
Ici, c’est le \(T\) qui joue ce rôle. Il intervient dans les numérateurs et les dénominateurs des deux premiers quotients que vous recherchez.
\(\dfrac{T...}{T...} = \dfrac{T...}{T...} = \dfrac{...}{...}\)
Question 6
Si on remplace par les valeurs que l'on connait on obtient \(\dfrac{TN}{TS} = \dfrac{2,4}{165} = \dfrac{2}{SH}\).
L'égalité des produits en croix appliquées aux deux derniers quotients nous donne :
\(2,4 \times 2 = 165 \times SH \)
\(2,4 \times SH = 165 \times 2 \)
\(2 \times SH = 165 \times 2,4 \)
\(SH = 2 \times 2,4 \times 165\)
Lorsque \(\dfrac{a}{b} = \dfrac{c}{d}\) alors \(a \times d = b \times c\)
Question 7
\(2,4 \times SH = 165 \times 2\)
À combien est égal \(SH\), la hauteur de la pyramide ?
\(SH = \dfrac{2 \times24}{165} \approx 0,03 \) m.
\(SH = \dfrac{2,4 \times165}{2} = 198 \) m.
\(SH = \dfrac{2 \times165}{2,4} = 137,5 \) m.
\(SH = 2 \times 2,4 \times 165 = 792 \) m.
Divise chaque membre par \(2,4\) afin d’isoler \(SH\).
Question 8
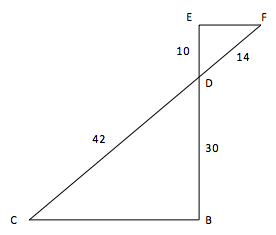
Les droites \((BE)\) et \((CF)\) se coupent en D.
On demande de prouver que les droites \((EF)\) et \((BC)\) sont parallèles.
Vous avez, bien sûr, dans l'idée dutiliser la réciproque du théorème de Thalès,
Mais pour cela, il faut commencer par vérifier l'égalité de deux quotients. Lesquels?
\(\dfrac{DB}{DE}\) et \(\dfrac{DC}{DF}\)
\(\dfrac{DB}{DF}\) et \(\dfrac{DC}{DE}\)
\(\dfrac{DB}{DE}\) et \(\dfrac{DF}{DC}\)
\(\dfrac{ED}{EB}\) et \(\dfrac{FD}{FC}\)
Commencez toujours par repérer le fameux « point-charnière ».
Ici, c’est le \(D\) qui joue ce rôle.
Les deux quotients sont donc \(\dfrac{D...}{D...}\) et \(\dfrac{D...}{D...}\)
Question 9
On va donc comparer \(\dfrac{DB}{DE}\) et \(\dfrac{DC}{DF}\).
\(\dfrac{DB}{DE} = \dfrac{30}{10} = 3\) et \(\dfrac{DC}{DF} = \dfrac{42}{14} = 3\)
\(\dfrac{DB}{DE} = \dfrac{30}{10} = \dfrac{15}{5}\) et \(\dfrac{DC}{DF} = \dfrac{42}{14} = \dfrac{21}{7}\)
\(\dfrac{DB}{DE}\) et \(\dfrac{DC}{DF}\) ne sont pas égaux.
Au secours ! Il me faut une calculatrice !
Il suffit de remplacer par les valeurs et de simplifier les fractions.
Question 10
\(\dfrac{DB}{DE}\) et \(\dfrac{DC}{DF}\) sont donc égaux (à 3).
Pour pouvoir enfin appliquer la réciproque du théorème de Thalès, il faut juste que vous écrivez l'autre hypothèse :
\((EF)\) et \((BC)\) sont parallèles.
\(EDF\) et \(DBC\) sont deux triangles.
\(C, D, F\) et \(B, D, E\) sont alignés.
\(C, D, F\) d’une part et \(B, D, E\) d’autre part sont alignés dans le même ordre.
Oui ! Souvenez-vous l’ordre des points est primordial !