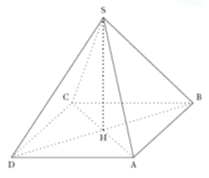
Un fabricant de cheminées contemporaines propose une cheminée régulière de base le carré $ABCD$, de côté $120 \ cm$. $H$ est le centre du carré.
La hauteur $[SH]$ de la pyramide mesure $80 \ cm$.
1) Le fabricant place sous la cheminée une plaque de fonte. Cette plaque a la forme d’un pavé droit de base $ABCD$ et d’épaisseur $1 \ cm$.
a) Justifier que son volume est $14 400 \ cm^3$.
b) La masse volumique de la fonte est $6,8 \ g/cm^3$. Quelle est la masse de cette plaque de fonte ?
2) a) On place le point $I$ milieu du segment $[AB]$.
On admettra que $HI = 60 \ cm$. Montrer que $SI = 100 \ cm$.
b) Les faces latérales de la pyramide sont en verre. Quelle est l’aire totale de la surface de verre de cette cheminée ?
1) a) La formule du volume d’un pavé droit est :
$V = l \times L \times h$ soit
$V = 120^2 \times 1 $
$V = 14400 \ cm^3$.
b) On a $6.8 = \dfrac{m}{14400}$ donc
$m = 14400 \times 6.8 = 97920 \ g = 97.92 \ kg$.
2) a) Le triangle $SHI$ est rectangle en $H$, d’après le théorème de Pythagore :
$SI^2 = SH^2 + HA^2 = 80^2 + 60^2 = 10 000$ donc
$SI = 100 \ cm$.
b) La pyramide $SABCD$ est une pyramide régulière donc chacune de ses faces est un triangle isocèle en $S$.
$I$ étant le milieu de $[AB]$, $(SI)$ est donc la médiane issue du sommet $S$ dans le triangle $SAB$ isocèle en $S$ mais aussi la hauteur issue de $S$.
Donc l’aire d’une face latérale est :
$A_L=\dfrac{AB \times SI}{2} $
$A_L= \dfrac{120 \times 100}{2} $
$A_L= 6 000 \ cm^2$.
L’aire totale de la surface de verre de cette cheminée est donc $4 \times 6 000$ soit $24 000 \ cm²$.
