L'énoncé
Dans toutes les questions, on se placera dans le pavé suivant.
$[Ox)$ est l'axe des abscisses, $[Oy)$ l'axe des ordonnées et $[Oz)$ l'axe des altitudes.
Tu as obtenu le score de
Question 1
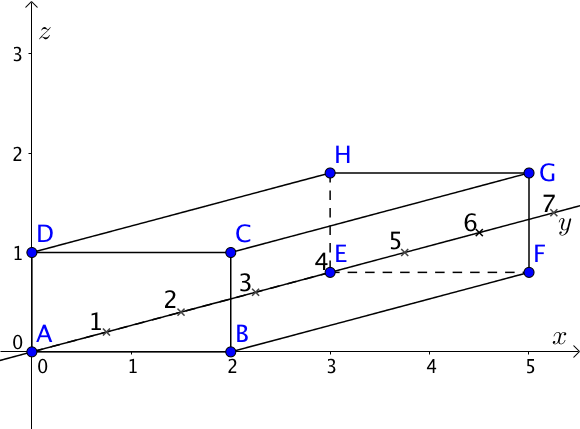
Quelles sont l'abscisse, l'ordonnée et l'altitude du point $A$ ?

abscisse : 0
ordonnée : 0
altitude : 0
abscisse : 0
ordonnée : 1
altitude : 0
abscisse : 0
ordonnée : 0
altitude : 1
Le point $A$ est confondu avec l'origine, il n'a donc aucune composante selon les différentes directions de l'espace.
Question 2
Quelles sont l'abscisse, l'ordonnée et l'altitude du point $B$ ?

abscisse : 0
ordonnée : 2
altitude : 0
abscisse : 0
ordonnée : 0
altitude : 2
abscisse : 2
ordonnée : 0
altitude : 0
Le point $B$ appartient à l'axe des abscisses, et on peut lire que son abscisse vaut 2, ainsi B est décrit dans le repère par
abscisse : 2
ordonnée : 0
altitude : 0
Question 3
Quelles sont l'abscisse, l'ordonnée et l'altitude du point $D$ ?

abscisse : 0
ordonnée : 0
altitude : 1
abscisse : 0
ordonnée : 1
altitude : 0
abscisse : 1
ordonnée : 0
altitude : 1
Le point $D$ appartient à la face latérale avant et appartient à la droite verticale de l'axe des altitudes, sur lequel on peut dire son altitude de 1. Ainsi, $D$ est repéré par
abscisse : 0
ordonnée : 0
altitude : 1
Question 4
Quelles sont l'abscisse, l'ordonnée et l'altitude du point $F$ ?

abscisse : 2
ordonnée : 0
altitude : 4
abscisse : 2
ordonnée : 4
altitude : 0
abscisse : 0
ordonnée : 4
altitude : 0
Le point $F$ appartient à la face inférieure, il n'a donc pas de composante selon l'altitude.
Les droites $(AE)$ et $(EF)$ étant perpendiculaires, les points $F$ et $E$ ont la même ordonnée, c'est à dire 4.
Les droites $(AB)$ et $(BF)$ étant perpendiculaires, les points $B$ et $F$ ont la même abscisse, c'est à dire 2.
Ainsi, $F$ est repéré par :
abscisse : 2
ordonnée : 4
altitude : 0
Question 5
Quelles sont l'abscisse, l'ordonnée et l'altitude du point $H$ ?

abscisse : 1
ordonnée : 4
altitude : 0
abscisse : 0
ordonnée : 1
altitude : 4
abscisse : 0
ordonnée : 4
altitude : 1
Le point $H$ appartient à la face latérale gauche, il n'a donc pas de composante selon l'axe des abscisses.
Pour atteindre le point $H$, on se déplace de $4$ dans la direction des ordonnées puis on monte de $1$ dans la direction de l'altitude, ainsi le point $H$ est repéré par :
abscisse : 0
ordonnée : 4
altitude : 1
