Voici les dimensions de quatre solides :
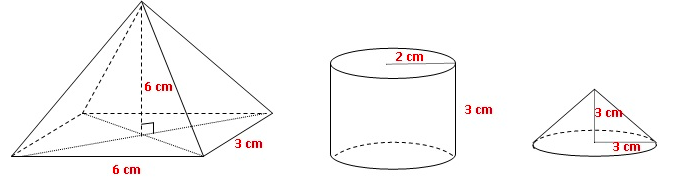
• Une pyramide de $6$ cm de hauteur dont la base est un rectangle de $6$ cm de longueur et de $3$ cm de largeur.
• Un cylindre de $2$ cm de rayon et de $3$ cm de hauteur.
• Un cône de $3$ cm de rayon et de $3$ cm de hauteur.
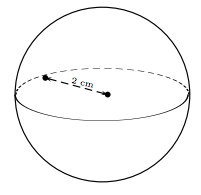
• Une boule de $2$ cm de rayon.
1) a) Représenter approximativement les trois premiers solides comme l’exemple ci-dessous :
b) Placer les dimensions données sur les représentations.
2) Classer ces quatre solides dans l’ordre croissant de leur volume. (On prendra $\pi=3,14$)
Quelques formules : $\dfrac{4}{3}\times \pi\times {\text{rayon}}^3$ $\pi\times {\text{rayon}}^2\times {\text{hauteur}} $
$\dfrac{1}{3}\times \pi\times {\text{rayon}}^2\times {\text{hauteur}} $ $\dfrac{1}{3}\times \text{aire de la base}\times {\text{hauteur}} $
Voici dans l'ordre croissant les quatre volumes :
$V_{Cône}= \dfrac{\text{aire de base} \times \text{hauteur}}{3} =\dfrac{3,14 \times 3^2 \times 3 }{3}\approx28,3$ cm3.
$V_{Boule} =\dfrac{4}{3}\pi \times \text{rayon}^3= \dfrac{4}{3}\times 3,14 \times 2^3 \approx 33,5 $cm3.
$V_{Pyramide}=\dfrac{1}{3}\times \text{aire de la base}\times {\text{hauteur}}=\dfrac{1}{3}\times 6 \times 3 \times 6 =36 $cm3.
$V_{Cylindre}=\pi\times {\text{rayon}}^2\times {\text{hauteur}}= 3,14 \times 2^2 \times 3 \approx 37,7 $cm3.
