L'énoncé
On considère sur la terre, quatre points $A, B, C, D$ et on connait les coordonnées géographiques des points $A$ et $B$ :
$A : 36°S \,12°W$ et $B : 51°N \,137°E$
Question 1
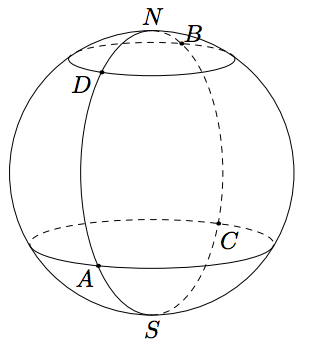
Déterminer les coordonnées géographiques des points $C$ et $D$ définis ci-dessous.
$C$ a la longitude de $B$ car ils sont sur le même méridien.
$C$ a la même latitude que $A$ car ils sont sur le même parallèle.
On en déduit : $C : 36S\, ; 137E$
De même, $D : 51N\,; 12W$
Repérer les points ayant les même latitudes ou longitudes
Question 2
La Terre qui est assimilée à une sphère de $6 371$ km de rayon.
Calculer le périmètre $P$ de l'équateur à $10$ km près.
ON connait la formule du périmètre d'un cercle :
$P=2\times \pi\times r$ où $r$ est le rayon de la terre.
Ainsi :
$P=2\times \pi\times 6371$
$P\approx 40030$
Le périmètre de la terre vaut environ $40030$km (souvent arrondi à $40000$ km dans les exercices)
$P=2\times \pi\times r$
Question 3
On cherche la longueur du parallèle passant par $D$, représenté ici par le petit cercle rouge.
La latitude de $D$ est symbolisée par l'angle de $51°$ (Nord).
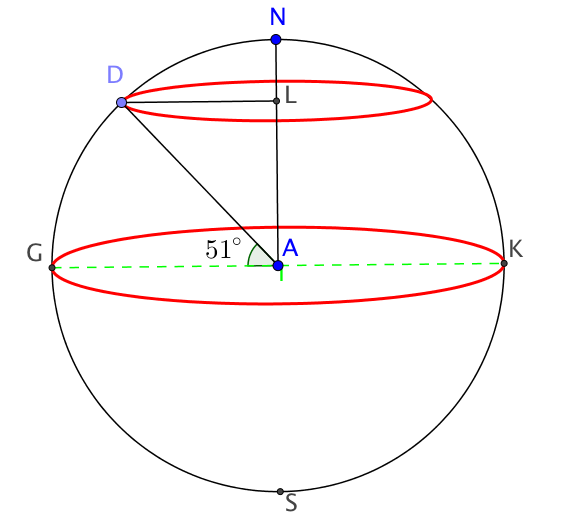
Le grand cercle rouge représente l'équateur et on rappelle que $AG=6371$km
Donner une valeur exacte de $DL$ puis une valeur approchée à $10$km près.
Pour déterminer le rayon $DL$ du parallèle, il faut au préalable travailler dans le triangle $ADL$.
On a $AG=AD$ donc :
$DL= AD\times \cos(\widehat{DAG})$
$DL=6371\times \cos(51)$
$DL\approx 4010$ km
Utiliser les relations trigonométriques dans un triangle rectangle
Question 4
En déduire une longueur $P$ approchée du parallèle passant par $D$ à $10$ km près.
On a :
$P=2\times \pi\times DL$
$P=2\times \pi\times 6371\times \cos(51)$
$P\approx 25190$
La longueur du parallèle vaut donc environ $25190$ km.
