Fiche de cours
Image d'un nombre par une fonction
Notion intuitive d'image
Considérons la courbe de température suivante :
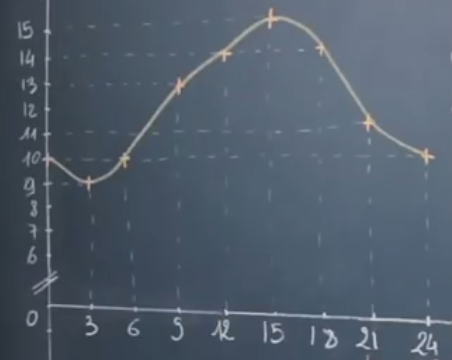
L'ensemble de définition de la fonction est $[0, 24]$, c'est à dire que l'étude se fait sur une journée complète à partir de minuit.
L'ordonnée est la température, il s'agit donc de la représentation graphique de la température en fonction du temps.
Ainsi, le temps est sur l'axe des abscisses.
Question : quelle température faisait-il à 3h du matin ?
On lit graphiquement que la température à 3h du matin est 9°C.
Ainsi, on dira que l'image de 3 par la fonction $f$ vaut 9 : il n'y a plus d'unité. On notera aussi $f(3) = 9$.
Définition
Soit $f$ une fonction et $a$ et $b$ deux réels vérifiants $f(a)=b$.
On dit que $b$ est l'image de $a$ par $f$.
Ou encore : l'image de $a$ par $f$ vaut $b$.
Autre exemple :
Pour trouver l'image de 15, on se place sur l'axe des abscisses à $t = 15$ puis on trace la droite perpendiculaire à cet axe et on regarde l'ordonnée du point d'intersection entre cette droite et la courbe de $f$ :
On lit $f(15) = 15$.
