La courbe $(C_1)$ ci-dessous représente, dans un repère orthonormé, une fonction $f$ définie et deux fois dérivable sur $[−1 ; 2]$.
On note $f ′$ la fonction dérivée de $f$ et $f ′′$ la fonction dérivée seconde de $f$ . La courbe ($C_2$) ci-dessous représente, dans le repère orthonormé, la fonction $f ′′$ .
Le point $A(0; 1)$ est situé sur la courbe ($C_1$). Le point $B$ est le point d’intersection de ($C_2$) avec l’axe des abscisses. Une valeur approchée de l’abscisse de $B$ est $0,37$. La tangente à la courbe ($C_1$) au point $A$ est horizontale.
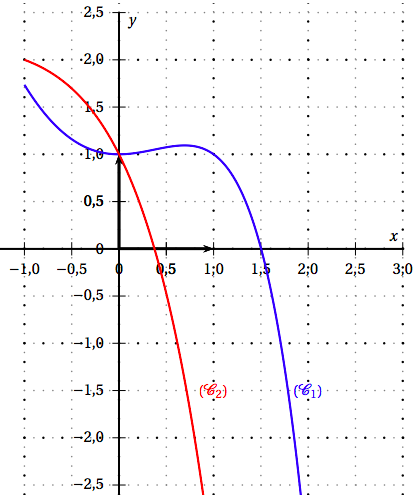
1. Par lecture graphique,
a. Donner la valeur de $f (0)$.
b. Donner la valeur de $f ′ (0)$.
c. Étudier la convexité de $f$ sur $[−1 ; 2]$. Justifier la réponse.
2. On admet désormais que la fonction $f$ est définie pour tout réel $x$ dans $[−1 ; 2]$ par : $f (x) = (1− x)e^x + x^2$ .
Un logiciel de calcul formel donne les résultats suivants :
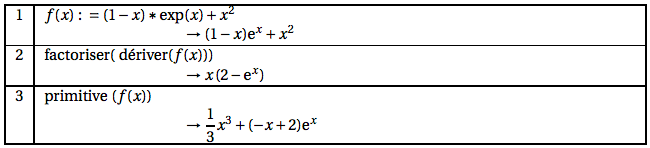
a. Vérifier le résultat trouvé par le logiciel pour le calcul de $f ′ (x)$.
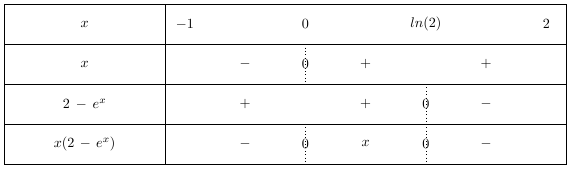
b. Étudier le signe de $f ′ (x)$ puis dresser le tableau de variation de la fonction $f$ sur $[−1 ; 2]$.
3. a. Justifier que l’équation $f (x) = 0$ possède une unique solution $\alpha$ dans $[−1 ; 2]$.
b. Déterminer un encadrement de $\alpha$ d’amplitude $0,01$.
4. Déterminer une équation de la tangente à ($C_1$) au point d’abscisse 1.
5. a. Justifier la ligne 3 du tableau de calcul formel.
b. On admet que la fonction $f$ est positive sur $[−1 ; 1]$. En déduire l’aire exacte, en unités d’aire, du domaine compris entre la courbe ($C_1$), l’axe des abscisses et les droites d’équation $x = −1$ et $x = 1$, puis en donner une valeur arrondie au dixième.
1 a. Le point $A (0 ; 1)$ appartient à $Cf$ donc $f (0) = 1$.
b. La tangente à $C_1$ au point $A$ est horizontale donc $f ′ (0) = 0$.
c. La fonction $f$ est convexe sur l’intervalle sur lequel la dérivée seconde $f ′′$ est positive.
D’après le graphique :
• $f ′′ > 0$ sur $[−1 ; 0,37[$ donc la fonction $f$ est convexe sur $[−1 ; 0,37[$;
• $f ′′ < 0$ sur $]0,37 ; 2]$ donc la fonction $ f$ est concave sur $]0,37 ; 2]$.
2 a. On a : $f (x) = (1− x) e^x + x^2$ donc
$f ′ (x) = (−1)× e ^x +(1− x)× e ^x +2x $
$ f′ (x)= − e ^x + e ^x − x e ^x +2x = 2x − x e ^x $
$ f′ (x)= x (2− e ^x ) $
$2− e ^x > 0 \iff 2> e ^x \iff \ln(2) > x$
On détermine le signe de $f ′ (x)$ au moyen d’un tableau de signes :
$f (−1) = 1+2 e −1 ≈ 1,74$;
$f (0) = 1$ ; $f (\ln(2)) ≈ 1,09$ et
$f (2) = 4− e^2 ≈ −3,39$
On dresse le tableau de variation de $f$ sur $[−1 ; 2]$ :

3. a. La fonction admet $1$ pour minimum sur $[-1;\ln(2)]$ donc elle ne s'annule pas.
La fonction $f$ est continue et strictement décroissante sur $[\ln(2);2]$. De plus, $f (\ln(2)) ≈ 1,09 > 0$ et $f (2) ≈ −3,39 < 0$
D’après le théorème des valeurs intermédiaires, on peut déduire que l’équation $f (x) = 0$ admet une solution unique $\alpha$ sur $] \ln(2) ; 2[$.
b. En utilisant la calculatrice, on trouve : $\alpha \in [1,50 ; 1,51]$
4. La tangente à une courbe représentant une fonction $f$ au point d’abscisse $a$ a pour équation $y = f ′ (a)(x − a)+ f (a)$.
Pour $a = 1 : f (1) = 1$ et $f ′ (1) = 2− e$
Donc la tangente a pour équation $y = (2− e ) (x −1)+1$ , c’est-à-dire :
$y = (2− e ) x −2+ e +1$ ou encore $y = (2− e ) x + e −1$.
5) a. La ligne 3 du tableau de calcul formel donne une primitive de la fonction $f$ ; on l’appelle $F$ et on a donc $F(x) =\dfrac{1}{3}x^3 +(−x +2) e ^x $
On va vérifier que $F ′ (x) = f (x)$ :
$F ′ (x) =\dfrac{1}{3}\times 3x^2 +(−1)× e ^x +(−x +2)× e ^x $
$F ′ (x)= x^2 + e ^x (−1− x +2) $
$F ′ (x)= (1− x) e ^x + x^2$
$F ′ (x)= f (x)$
b. D’après le cours, elle vaut, en unités d’aire :
$A = \displaystyle\int_{-1}^{1} f(x)dx = F(1)−F(−1) $
$A=\left[\dfrac{1}{3} +(2−1) e^1\right]-\left[\dfrac{1}{3}\times (-1) +(2−(−1)) e^{−1}\right]$
$A ≈ 2,3$ u.a