L'énoncé
On considère un cube \(ABCDEFGH\) d’arête de longueur 1.
On note \(I\) le centre de la face \(ADHE\); \(J\) celui de la face \(ABCD\) et \(K\) le milieu du segment \([IJ]\).
L’espace est rapporté au repère orthonormal \((A ; \overrightarrow{AB} ,\overrightarrow{AD}, \overrightarrow{AE})\).
Question 1
Déterminer les coordonnées des points \(I\), \(J\) et \(K\) dans ce repère. Une figure est conseillée.
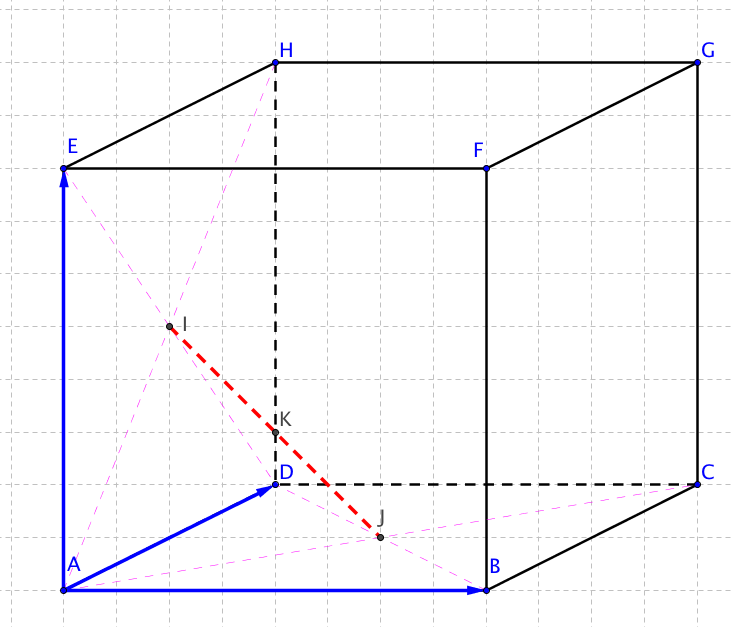
\(\overrightarrow{AI} = \dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AE}\)
Donc : \(I(0 ; 0,5 ; 0,5)\)
\(\overrightarrow{AJ} = \dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
Donc \(J(0,5 ; 0,5 ; 0)\)
\(K\) est le milieu de \([IJ]\) donc \(K\) a pour coordonnées : \(K(0,25 ; 0,5 ; 0,25)\)
Commencez par chercher les coordonnées des sommets du cube dans ce repère.
Cherchez une égalité vectorielle du vecteur \(\overrightarrow{AI}\) en fonction des vecteurs de la base.
Connaissez-vous la formule donnant les coordonnées du milieu d’un segment ?
Question 2
Démontrer que les points \(A\), \(K\) et \(G\) ne sont pas alignés.
\(\overrightarrow{AG}\) a pour coordonnées \((1;1;1)\).
\(\overrightarrow{AK}\) a pour coordonnées \((0,25;0,5;0,25)\) donc il n'existe pas de réel \(k\) tel que \(\overrightarrow{AK} = k\overrightarrow{AG}\).
Les points \(A\), \(K\) et \(G\) ne sont pas alignés.
Calculez les coordonnées des vecteurs \(\overrightarrow{AG}\) et \(\overrightarrow{AK}\).
Montrez qu’ils ne sont pas colinéaires.
Concluez.
Question 3
Démontrer que le plan médiateur du segment \([IJ]\) est le plan \((AKG)\).
\(AI^2 = 0.5^2+0.5^2 = 0.5\) et \(AJ^2 = 0.5^2+0.5^2 = 0.5\) donc :
\(AI = AJ\) Et \(A\) appartient au plan médiateur du segment \([IJ]\).
\(KI^2 = 0.25^2+0.25^2 = 0.125\) et \(KJ^2 = 0.25^2+0.25^2 = 0.125\) donc :
\(KI = KJ\) Et \(K\) appartient au plan médiateur du segment \([IJ]\).
\(GI^2 = 1^2+0.5^2+0.5^2 = 1.5\) et \(GJ^2 = 0.5^2+0.5^2+1^2 = 1.5\) donc :
\(GI = GJ\) Et \(G\) appartient au plan médiateur du segment \([IJ]\).
Les points \(A\), \(K\) et \(G\) ne sont pas alignés donc le plan médiateur du segment \([IJ]\) est le plan \((AKG)\).
On rappelle ce qu’est un plan médiateur d'un segment \([IJ]\) :
C'est l'ensemble des points \(M\) de l'espace vérifiant \(MI=MJ\).
Comparez les longueurs \(AI\) et \(AJ\). (comparez plutôt \(AI^2\) et \(AJ^2\), c’est plus facile et équivalent car ce sont des longueurs donc positives). Concluez pour le point \(A\).
Faites le même travail pour \(K\) et \(G\).
Concluez.
Question 4
Déterminer une équation cartésienne du plan \((AKG)\).
Le plan médiateur du segment \([IJ]\) est le plan \((AKG)\) donc \(\overrightarrow{IJ}(0,5 ; 0 ; - 0,5)\) ou encore \(\overrightarrow{n} (1 ; 0 ; -1)\) est un vecteur normal au plan \((AKG)\).
Une équation de \((AKG)\) est donc de la forme \(x - z + d = 0\)
\(A\) appartient à ce plan donc \(d = 0\).
Conclusion :
Une équation cartésienne du plan \((AKG)\) est \(x - z = 0\)
Cherchez un vecteur normal à \((AKG)\).
Utilisez la question précédente pour cela.
Cherchez à présent une équation cartésienne du plan. Un oubli ? Allez voir la vidéo dans les prérequis.
Question 5
Vérifier que le point \(D\) appartient au plan \((AKG)\).
\(D\) a pour coordonnées \((0 ; 1 ; 0)\) donc \(x_D - z_D = 0\)
Ainsi, le point \(D\) appartient au plan \((AKG)\).
Remplacez les coordonnées de \(D\) dans l’équation du plan \((AKG)\). Concluez.
