Fiche de cours
Produit scalaire dans l'espace
Rappel : Vecteurs colinéaires
Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires si et seulement si il existe un réel $\lambda$ tel que $\overrightarrow{u}=\lambda\overrightarrow{v}$.
Exemple :
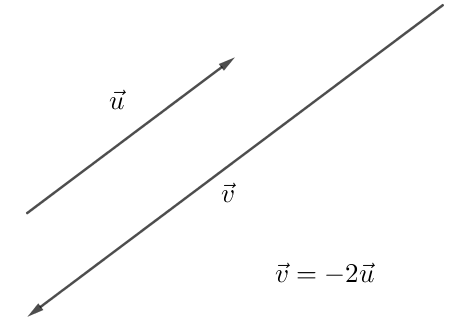
Propriétés
Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ colinéaires et non nuls ont la même direction.
Trois points $A$, $B$ et $C$ sont alignés si et seulement si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.
Le vecteur nul est colinéaire à tout autre vecteur.
Exemple
Les vecteurs $\overrightarrow{u}(2;3;1)$ et $\overrightarrow{v}(-6;9;-3)$ sont colinéaires car $\overrightarrow{v}=-3\times\overrightarrow{u}$.
Les vecteurs $\overrightarrow{u}(2;-3;1)$ et $\overrightarrow{v}(4;-6;-2)$ ne sont pas colinéaires car
$2\times 2=4$ ; $2\times(-3)=-6$ mais $2\times 1\neq -2$.
Produit scalaire, Définition
Dans l'espace, une unit&eacu
