L'énoncé
L’espace est rapporté à un repère orthonormal \((O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k})\).
On considère les points \(A(3 ; 4 ; 0)\) ; \(B (0 ; 5 ; 0)\) et \(C (0 ; 0 ; 5)\).
On note \(I\) le milieu du segment \([AB]\).
Question 1
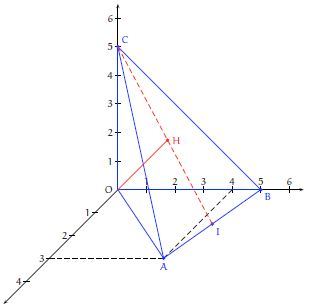
Faire une figure où l'on placera les points \(A\), \(B\), \(C\) et \(I\) dans le repère \((O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k})\).
Question 2
Démontrer que les triangles \(OAC\) et \(OBC\) sont rectangles et isocèles.
Quelle est la nature du triangle \(ABC\) ?
\(OA = \sqrt{3^2 + 4^2} = \sqrt{25} = 5 = OC\) et donc le triangle \(OAC\) est isocèle en \(O\).
\(\overrightarrow{OA}.\overrightarrow{OC} = 3 \times 0 + 4 \times 0 + 0 \times 5 = 0\) et donc le triangle \(OAC\) est rectangle en \(O\).
On montre de la même façon que \(OB = OC = 5\) et que \(\overrightarrow{OB}.\overrightarrow{OC} = 0\).
Donc le triangle \(OBC\) est rectangle et isocèle en \(O\).
On en déduit que \(AC = BC = OC\sqrt{2} = 5\sqrt{2}\) et le triangle \(ABC\) est isocèle en \(C\).
D'autre part, \(AB = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2 + (z_B - z_A)^2} = \sqrt{1^2 + 3^2} = \sqrt{10}\)
Comme \(\sqrt{10} \neq 5\sqrt{2}\), le triangle \(ABC\) n'est pas équilatéral.
Comme \(AC\sqrt{2} = 10 \neq \sqrt{10} = AB\), le triangle \(ABC\) n'est pas isocèle rectangle.
Pour chaque triangle isocèle, deux calculs de longueur suffisent.
Pour l’angle droit, pensez au produit scalaire.
Deux vecteurs sont orthogonaux lorsque leur produit scalaire est nul.
Pour \(ABC\), commencez à vous demander s’il est isocèle, équilatéral ou rectangle.
Question 3
Soit \(H\left(\dfrac{15}{19};\dfrac{45}{19};\dfrac{45}{19}\right)\)
Démontrer que les points \(H\), \(C\) et \(I\) sont alignés.
Le point \(I\) a pour coordonnées \(\left(\dfrac{x_A+x_B}{2}, \dfrac{y_A+y_B}{2}, \dfrac{z_A+z_B}{2}\right)\) ou encore \(I\left( \dfrac{3}{2} ; \dfrac{9}{2} ; 0\right)\)
Le vecteur \(\overrightarrow{CI}\) a pour coordonnées \((x_I - x_C, y_I - y_C, z_I - z_C)\) ou encore \(\overrightarrow{CI}\left( \dfrac{3}{2} ; \dfrac{9}{2} ; -5\right)\)
D'autre part, le vecteur \(\overrightarrow{CH }\) a pour coordonnées \(\overrightarrow{CH }\left( \dfrac{15}{19} ; \dfrac{45}{19} ; -\dfrac{50}{19}\right)\)
On en déduit que \(\overrightarrow{CI} = \dfrac{19}{5 \times 2}\overrightarrow{CH}\)
Ainsi, les vecteurs \(\overrightarrow{CI}\) et \(\overrightarrow{CH}\) sont colinéaires et donc les points \(H\), \(C\) et \(I\) sont alignés.
Commencez par trouver les coordonnées de \(I\).
Calculez ensuite par exemple les coordonnées des vecteurs \(\overrightarrow{CI}\) et \(\overrightarrow{CH}\).
Si les coordonnées sont proportionnelles, les vecteurs sont colinéaires.
Question 4
Démontrer que \(H\) est le projeté orthogonal de \(O\) sur le plan \((ABC)\).
Les points \(C\) et \(I\) sont dans le plan \((ABC)\). On en déduit que la droite \((CI)\) est contenue dans le plan \((ABC)\).
Puisque le point \(H\) appartient à la droite \((CI)\), le point \(H\) est dans le plan \((ABC)\).
D'autre part, le vecteur \(\overrightarrow{OH}\) a pour coordonnées :\(\overrightarrow{OH}\left(\dfrac{15}{19}, \dfrac{45}{19}, \dfrac{45}{19}\right)\)
Le vecteur \(\overrightarrow{BC}\) a pour coordonnées \(\overrightarrow{BC}(0,-5, 5)\)
Le vecteur \(\overrightarrow{AB}\) a pour coordonnées \(\overrightarrow{AB}(-3, 1, 0)\)
Ainsi : \(\overrightarrow{OH}.\overrightarrow{BC} = \dfrac{15}{19} \times 0 + \dfrac{45}{19} \times (-5) + \dfrac{45}{19} \times 5 = 0\)
Et : \(\overrightarrow{OH}.\overrightarrow{AB} = \dfrac{15}{19} \times(-3) + \dfrac{45}{19} \times 1 + \dfrac{45}{19} \times 0 = 0\)
Ainsi, la droite \((OH)\) est orthogonale aux droites \((BC)\) et \((BA)\) qui sont deux droites sécantes du plan \((ABC)\).
On en déduit que la droite \((OH)\) est perpendiculaire au plan \((ABC)\).
En résumé, le point \(H\) est dans le plan \((ABC)\) et la droite \((OH)\) est perpendiculaire au plan \((ABC)\).
Ceci montre que le point \(H\) est le projeté orthogonal du point \(O\) sur le plan \((ABC)\).
Montrez dans un premier temps que \(H\) appartient au plan \((ABC)\).
Vous pourrez utiliser le fait que \(H\) est un point de \((IC)\) pour montrer que \(H\) est un point de \((ABC)\).
Un vecteur est normal à un plan s’il est orthogonal à deux vecteurs non colinéaires du plan.
Calculez donc \(\overrightarrow{OH}.\overrightarrow{BC}\) et un autre produit scalaire que vous choisirez. Un produit scalaire nul traduit l’orthogonalité dans l’espace.
Question 5
En déduire une équation cartésienne du plan \((ABC)\).
Le plan \((ABC)\) est le plan passant par \(B\) et de vecteur normal \(\overrightarrow{OH}\).
Ainsi d'après le cours, on a :
\(\dfrac{15}{19}(x-0)+\dfrac{45}{19}(y-5)+\dfrac{45}{19}(z-0) = 0\)
Ou encore : \(x+3(y-5)+3z = 0\)
Ou enfin : \(x+3y+3z - 15=0\)
Une équation cartésienne du plan \((ABC)\) est donc : \(x + 3y + 3z - 15=0\).
On sait désormais que le vecteur \(\overrightarrow{OH}\) est un vecteur normal du plan. On va utiliser ses coordonnées pour trouver l’équation du, plan. Un oubli ? Voir la vidéo de rappel sur l'équation cartésienne du plan.
On utilise ensuite que \(B\) (par exemple) appartient à ce plan.
Question 6
Calculs d'aire et de volume
Calculer l'aire du triangle \(OAB\). En déduire le volume du tétraèdre \(OABC\).
La distance du point \(A\) au segment \([OB]\) est \(x_A = 3\) puisque le point $A$ est dans le plan d'équation $z=0$
Ainsi, l'aire du triangle \(OAB\) est : \(Aire_{OAB}=\dfrac{3 \times 5}{2} = \dfrac{15}{2} \;u.a\).
Puisque la droite \((OC)\) est perpendiculaire au plan \((OAB)\), le volume $V$ du tétraèdre \(OABC\) est :
\(V=\dfrac{Aire_{OAB} \times OC}{3} = \dfrac{\frac{15}{2} \times 5}{3} = \dfrac{75}{6}\)
Le volume du tétraèdre \(OABC\) est donc \(V = \dfrac{75}{6}\;u.v\)
Pour l’aire du triangle \(ABO\), une figure plane peut vous aider. Les coordonnées des points sont entières.
Un tétraèdre est une pyramide à base triangulaire. Vous connaissez donc la formule du volume.
\(OC\) est la hauteur associée à ce calcul de volume. En effet les axes sont orthogonaux les uns avec les autres.
Question 7
Déterminer la distance du point \(O\) au plan \((ABC)\).
Première solution :
Puisque le point \(H\) est le projeté orthogonal du point \(O\) sur le plan \((ABC)\), la distance de \(O\) au plan \((ABC)\) est la distance \(OH\).
\(OH = \sqrt{\left( \dfrac{15}{19} \times 1 \right)^2 + \left( \dfrac{15}{19} \times 3 \right)^2 + \left( \dfrac{15}{19} \times 3 \right)^2 }\)
\(OH = \sqrt{ \left(\dfrac{15}{19}\right)^2 \times (1^2+3^2+3^2)}\)
\(OH = \dfrac{15}{19}\sqrt{1^2+3^2+3^2}\)
\(OH = \dfrac{15\sqrt{19}}{19}\)
Ou encore : \(OH = \dfrac{15}{\sqrt{19}}\)
Deuxième solution :
Une équation cartésienne du plan \((ABC)\) est \(x+3y+3z-15 = 0\)
Et donc, d'après le cours, la distance du point \(O\) au plan \((ABC)\) est :
\(d = \dfrac{|0 + 0 + 0 - 15|}{\sqrt{1^2 + 3^2 + 3^2}} = \dfrac{15}{\sqrt{19}} \)
La distance du point \(O\) au plan \((ABC)\) est donc : \(d = \dfrac{15}{\sqrt{19}}\)
Il y a deux méthodes pour résoudre cette question.
Soit vous remarquez que la distance que vous recherchez est \(OH\) et vous calculez la distance avec la formule de la distance entre deux points.
Vous pouvez aussi utiliser la formule du cours qui vous donne la distance d’un point à un plan.
Question 8
Calculer l'aire du triangle \(ABC\).
On sait que \(V = \dfrac{Aire_{ABC} \times d}{3}\)
Ainsi : \(Aire_{ABC} = \dfrac{3V}{d} = \dfrac{\frac{75}{6} \times 3}{\frac{15}{\sqrt{19}}}\)
\(Aire_{ABC}= \dfrac{5 \times 15 \times 3}{2 \times 3} \times \dfrac{\sqrt{19}}{15} = \dfrac{5\sqrt{19}}{2}\)
L'aire du triangle \(ABC\) est donc : \(Aire_{ABC}=\dfrac{5\sqrt{19}}{2}u.a\)
On connait le volume du tétraèdre. On peut l’exprimer de quatre façons différentes selon l’aire de base que l’on choisit.
Dans la question 4a), on a choisi \(OAB\) comme aire de base.
Quelle hauteur pouvez-vous choisir si vous voulez qu’\(ABC\) soit l’aire de base ?
