L’espace est muni d’un repère orthonormé $(O; \vec{i},\vec{j},\vec{k}).$
Soit $P$ le plan d’équation cartésienne : $2x − z − 3 = 0.$
On note $A$ le point de coordonnées $(1 ; a ; a^2),$ où $a$ est un nombre réel.
2) a) Déterminer une représentation paramétrique de la droite $D$ (de paramètre noté $t$) passant par le point $A$ et orthogonale au plan $P.$
b) Soit $M$ un point appartenant à la droite $D,$ associé à la valeur $t$ du paramètre dans la représentation paramétrique précédente.
Exprimer la distance $AM$ en fonction du réel $t.$
On note $H$ le point d’intersection du plan $P$ et de la droite $D$ orthogonale à $P$ et passant par le point $A.$ Le point $H$ est appelé le projeté orthogonal du point $A$ sur le plan $P,$ et la distance $AH$ est appelée distance du point $A$ au plan $P.$
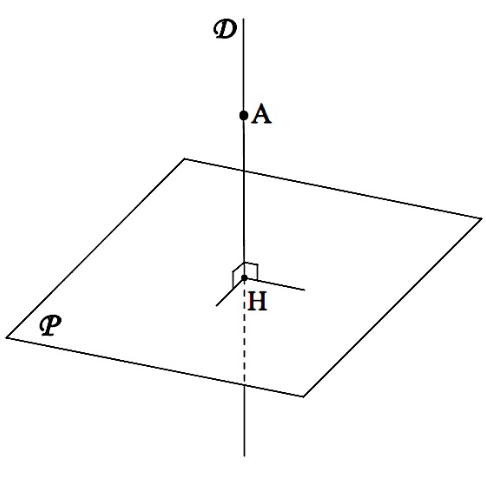
3) Existe-t-il une valeur de $a$ pour laquelle la distance $AH$ du point $A$ de coordonnées $(1 ; a ; a^2)$ au plan $P$ est minimale ? Justifier la réponse.
