Lors d'un match de rugby, un joueur doit transformer un essai qui a été marqué au point $E$ (voir figure ci-dessous) situé à l’extérieur du segment $[AB]$.
La transformation consiste à taper le ballon par un coup de pied depuis un point $T$ que le joueur a le droit de choisir n’importe où sur le segment $[EM]$ perpendiculaire à la droite $(AB)$ sauf en $E$. La transformation est réussie si le ballon passe entre les poteaux repérés par les points $A$ et $B$ sur la figure.
Pour maximiser ses chances de réussite, le joueur tente de déterminer la position du point $T$ qui rend l'angle $\widehat{ATB}$ le plus grand possible.

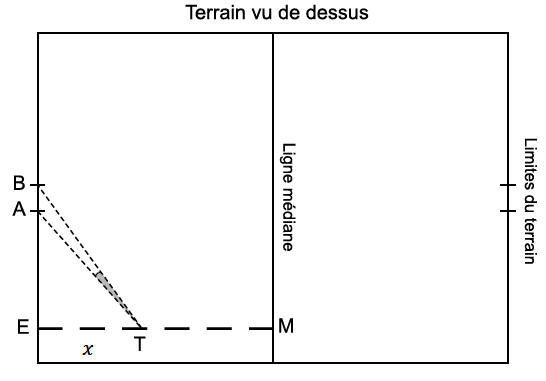
Le but de cet exercice est donc de rechercher s'il existe une position du point $T$ sur le segment $[EM]$ pour laquelle l’angle $\widehat{ATB}$ est maximum et, si c'est le cas, de déterminer une valeur approchée de cet angle.
Dans toute la suite, on note $x$ la longueur $ET$, qu’on cherche à déterminer.

Les dimensions du terrain sont les suivantes : $EM = 50 \ m$, $EA = 25 \ m$ et $AB = 5,6 \ m$. On nota $\alpha$ la mesure en radian de l'angle $\widehat{ETA}$, $\beta$ la mesure en radian de l'angle $\widehat{ETB}$ et $\gamma$ la mesure en radian de l'angle $\widehat{ATB}$.

1) En utilisant les triangles rectangles $ETA$ et $ETB$ ainsi que les longueurs fournies, exprimer $\tan \alpha$ et $\tan \beta$ en fonction de $x$.

La fonction tangente est définie sur l'intervalle $\left \rbrack {0 ; \dfrac{\pi}{2}} \right \lbrack$ par $\tan x = \dfrac{\sin x}{\cos x}$.

2) Montrer que la fonction $\tan$ est strictement croissante sur l'intervalle $\left \rbrack {0 ; \dfrac{\pi}{2}} \right \lbrack$.

3) L'angle $\widehat{ATB}$ admet une mesure $\gamma$ appartenant à l'intervalle $\left \rbrack {0 ; \dfrac{\pi}{2}} \right \lbrack$, résultat admis ici, que l'on peut observer sur la figure.

On admet que, pour tous réels $a$ et $b$ de l'intervalle $\left \rbrack {0 ; \dfrac{\pi}{2}} \right \lbrack$, $\tan (a-b) = \dfrac{\tan a - \tan b}{1+ \tan a \times \tan b}$.

Montrer que $\tan \gamma = \dfrac{5,6 x}{x^2 + 765}$.

4) L'angle $\widehat{ATB}$ est maximum lorque sa mesure $\gamma$ est maximale. Montrer que cela correspond à un minimum sur l'intervalle $\left \rbrack {0 ; 50} \right \rbrack$ de la fonction $f$ définie par : $f(x) = x + \dfrac{765}{x}$.

Montrer qu'il existe une unique valeur de $x$ pour laquelle l'angle $\widehat{ATB}$ est maximum et déterminer cette valeur de $x$ au mètre près ainsi qu'une mesure de l'angle $\widehat{ATB}$ à $0,01$ radian près.

Remarque : sur un terrain, un joueur de rugby ne se soucie pas d'une telle précision !