Fiche de cours
Dérivée seconde et position d'une courbe par rapport à ses tangentes
Soit $f$ une fonction deux fois dérivable sur un intervalle $I$ et $x_0 \in I$.
Soit $\Gamma_f$ la courbe représentative de la fonction $f$ dans le repère $(O; \overrightarrow{i}; \overrightarrow{j})$ et $M_O(x_0, f(x_0))$.
On note $\Delta$ la tangente à $\Gamma_F$ en $M_0$ (cette tangente existe car $f$ est dérivable en $x_0$).
Soit $x \in I$ et $M(x, f(x))$,
Soit $T$ le point de $\Delta$ tel que $T(x, y_T)$,
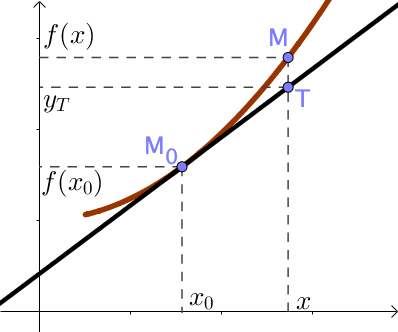
On étudie ici la position de la courbe par rapport à sa tangente en un point d'abscisse $x_0$ quelconque. Pour cela, on étudie l'ordonnée du vecteur $\overrightarrow{TM}$ (l'abscisse du vecteur étant nulle) à partir d'un point $M$ quelconque :
$y_\overrightarrow{TM} = y_M - y_T = f(x) - y_T$.
Or $T$ est un point de la tangente $\Delta$ dont on connait l'équation :
$y = f(x_0) + (x - x_0)f'(x_0)$.
Ainsi, $y_T = f(x_0) + (x - x_0)f'(x_0)$.
Finalement, $y_\overrightarrow{TM} = f(x) - f(x_0) - (x - x_0)f'(x_0)$.
On note alors $\delta(x) = f(x) - f(x_0) - (x - x_0)f'(x_0)$ et on étudie le signe de cette fonction. Pour cela, on ét
