Fiche de cours
$n$-uplets de $(0, 1)$
On s'intéresse ici au nombre de $n$ uplets ($n \in \mathbb{N}^*$) pouvant être construits à partir de $2$ éléments : 0 et 1.
Un exemple de $n$-uplet est $(0, 1, 1, 0, ..., 1)$.
On remarque alors que l'ordre d'apparition doit être considéré et qu'il peut y avoir répétition.
Pour chaque élément du $n$-uplet, il existe deux choix possibles (0 ou 1).
En appliquant le principe multiplicatif pour les $n$ éléments, on trouve qu'il existe $\underbrace{2 \times 2 \times ... \times 2}_{n} = 2^n$ $n$-uplets de $\{0; 1\}$.
Exemples :
On considère dans un premier temps un alphabet à 2 lettres. Un mot de $n$ lettres est un $n$-uplet.
Il y a donc $2^n$ mots de $n$ lettres lorsqu'il existe deux lettres dans l'alphabet.
On peut aussi s'intéresser à un arbre avec deux choix possibles à chaque étape. On se demande le nombre de chemins que l'on peut parcourir en partant de la racine jusqu'à l'extrémité d'une des feuilles.
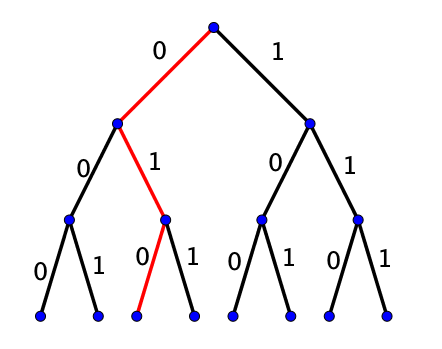
Pour se faire, on remarque qu'à chaque arrêt, il existe deux choix possibles : suivre le chemin de gauche, que l'on symbolise par un 0, ou alors le chemin de droite, symbolisé par un 1.
Un chemin peut être assimilé à un $3$-uplet (ou triplet).
Ainsi, le nombre de chemins possibles correspond au nombre de $n$ uplets que l'on peut former avec des $0$ et des $1$.
Puisque $n = 3$ dans l'exemple, il y a donc $2^3 = 8$ chemins possibles.
Enfin, le dernier exemple traite de la répétition de $n$ épreuves de Bernoulli ayant deux issues $\{0; 1\}$ (Succès ou Echec).
La répétition peut être codée par un $n$-uplet représentant chacun des choix à l'issue des $n$ épreuves.
Le nombre de répétitions est le même que le nombre de $n$-uplets constitués de $0$ ou de $1$, à savoir $2^n$.
