L'énoncé
Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1

$\Omega$ se compose des ensembles A et B.
A quoi correspond $|A\cup B|$ ?
$|A|+|B|$
$|A|+|B|-|A\cap B|$
$|A|+|B|-|A\cup B|$
C'est une question de cours.
Question 2

Les ensembles A,B,C sont contenus dans $\Omega$.
A quoi correspond $|A\cup B\cup C|$ ?
$|A|+|B|+|C|$
$|A|+|B|+|C|-|A\cap B\cap C|$
$|A|+|B|+|C|-|A\cap B\cap C|-|A\cup B\cup C|$
$|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$
Attention à ne pas oublier le terme $|A\cap B\cap C|$
Question 3
Quelle(s) situation(s) de dénombrement correspond(ent) au principe additif ?
Le nombre d'élèves dans une classe sachant que 20 étudient l'allemand, 24 l'anglais et 5 étudient les deux langues.
Le nombre de menus dans un restaurant sachant qu'ils se composent à partir de 5 entrées, 5 plats et 5 desserts.
Le nombre de codes possibles sur un boîtier sachant qu'un code se compose de 4 chiffres.
Le nombre de billes dans un sac contenant des billes rouges, bleues et bicolores sachant qu'il y a 27 billes qui contiennent du rouge, 5 qui contiennent du bleu et 5 qui sont bicolores.
Question 4
Soit un ensemble $\Omega$ composé de 3 sous-ensembles A, B et C.
On a $|\Omega |=|A|+|B|+|C|$ seulement si :
Tous les éléments sont rangés dans l'ordre croissant
Tous les éléments sont comptés une et une seule fois
A, B et C sont 2 à 2 distincts.
$A\cup B\cup C=\Omega$
Question 5
Dans un tiroir, 23 chaussettes contiennent du bleu, 21 contiennent du rouge et 12 sont bicolores. Combien y-a-t-il de chaussettes ?
28
32
44
On pourra s'aider du diagramme de Venn suivant :
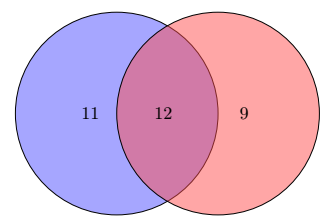
Question 6
Prenons un boitier contenant tous les chiffres de 0 à 9 permettant de réaliser un code à 4 chiffres.
Combien de code peut-on composer ?
1000
6561
9999
10000
Pour chaque chiffre on a 10 choix.
Il y a donc $10^4=10000$ possibilités.
On peut aussi voir cela de la manière suivante : il y a tous les nombres disponibles entre 0000 et 9999, donc 10000.
Question 7
Un costumier dispose de 20 pantalons, 20 chemises, 10 chapeaux et 5 capes.
Combien de déguisements peut-on réaliser si l'on prend 1 accessoire parmi chaque ?
1000
2000
8000
20000
$20\times 20\times 10\times 5=20000$
Question 8
Un autre costumier dispose de 20 pantalons, 20 chemises, 20 chapeaux et 10 capes.
Cependant, un costume se compose d'un pantalon au choix, d'une chemise au choix et d'un chapeau ou d'une cape.
Combien y-a-t-il de costumes possibles ?
12 000
18 000
40 000
80 000
Cette fois-ci, on combine le principe additif et multiplicatif.
Il y a 8 000 costumes qui contiennent un chapeau (20x20x20) et 4 000 qui contiennent une cape (20x20x10).
Les deux ensembles étant distincts on peut les additionner: il y a 12 000 costumes possibles.
Question 9
On pioche successivement 3 billes dans une urne de 18 billes numérotées avec remise.
Combien y a-t-il de tirages possibles avec ordre ?
6
324
4896
5832
Il y a $18$ choix possibles pour chaque tirage.
$18^3=2538$ choix possibles
Question 10
Soit 3 ensembles A, B , C.
L'ensemble $A\times B\times C$:
S'appelle le produit vectoriel des ensembles A, B, C.
S'appelle le produit cartésien des ensembles A, B, C.
Contient l'ensemble des éléments de A, B, C.
Est composé de tous les triplets formés à partir d'un élément de A, un élément de B, un élément de C.
