L’objet du problème est l’étude des intégrales $I$ et $J$ définies par : $I =\displaystyle \int_0^1 \dfrac{1}{1+x} dx$ et $J =\displaystyle \int_0^1 \dfrac{1}{1+x^2} dx$
Partie A : valeur exacte de l’intégrale $I$
1. Donner une interprétation géométrique de l’intégrale $I$.
2. Calculer la valeur exacte de $I$.
Partie B : estimation de la valeur de $J$
Soit $g$ la fonction définie sur l’intervalle $[0; 1]$ par $g (x) =\dfrac{1}{1+x^2} $.
On note $C_g$ sa courbe représentative dans un repère orthonormé du plan. On a donc : $J =\displaystyle \int_0^1 g(x)dx $
Le but de cette partie est d’évaluer l’intégrale $J$ à l’aide de la méthode probabiliste décrite ci-après.
On choisit au hasard un point $M (x ; y)$ en tirant de façon indépendante ses coordonnées $x$ et $y$ au hasard selon la loi uniforme sur $[0; 1]$. On admet que la probabilité $p$ qu’un point tiré de cette manière soit situé sous la courbe $C_g$ est égale à l’intégrale $J$.
En pratique, on initialise un compteur $c$ à $0$, on fixe un entier naturel $n$ et on répète $n$ fois le processus suivant :
— on choisit au hasard et indépendamment deux nombres $x$ et $y$, selon la loi uniforme sur $[0; 1]$;
— $si M (x ; y)$ est au-dessous de la courbe $C_g$ on incrémente le compteur $c$ de $1$. On admet que $f = \dfrac{c}{n}$ est une valeur approchée de $J$. C’est le principe de la méthode dite de MonteCarlo.
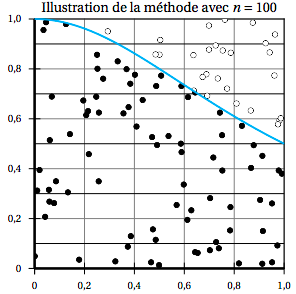
La figure ci-dessous illustre la méthode présentée pour $n = 100$.
$100$ points ont été placés aléatoirement dans le carré. Les disques noirs correspondent aux points sous la courbe, les disques blancs aux points au-dessus de la courbe. Le rapport du nombre de disques noirs par le nombre total de disques donne une estimation de l’aire sous la courbe.
1. Recopier et compléter l’algorithme ci-après pour qu’il affiche une valeur approchée de J.

2. Pour $n = 1000$, l’algorithme ci-dessus a donné pour résultat : $f = 0,781$. Donner un intervalle de confiance, au niveau de confiance de $95$ %, de la valeur exacte de $J$.
3. Quelle doit-être, au minimum, la valeur de $n$ pour que l’intervalle de confiance, au niveau de confiance de $95$ %, ait une amplitude inférieure ou égale à $0,02$ ?
On a : $x\in [0;1]$ ou encore $0\leq x \leq 1$
Ainsi : $1\leq x+1 \leq 2$
En passant à l'inverse : (la fonction décroissante sur $[1;2]$)
$\dfrac{1}{2} \leq \dfrac {1}{1+x}\leq 1$
On en conclut que $\dfrac {1}{1+x}\geq 0$ et que $J$ est aussi positive.
$J$ est donc l'aire (en unité d'aire) du domaine compris entre la courbe représentant la fonction $x\to\dfrac {1}{1+x}$ , l'axe des abscisses et les droites d'équations $x=0$ et $x=1$.
2) On sait que $x\to\dfrac {1}{1+x}>0$ donc la fonction $x\to\dfrac {1}{1+x}$ admet pour primitive $x\to \ln(x+1)$
Ainsi : $I= \left[\ln(x+1)\right]_0^1= \ln(2)-\ln(1)=\ln(2)$ u.a
Partie B
1) On complète l’algorithme :

2) Pour $n = 1000$, l’algorithme ci-dessus a donné pour résultat : $f = 0,781$.
L’intervalle de confiance, au niveau de confiance de $95$ % est :
$I=\left[f-\dfrac{1}{\sqrt n};f+\dfrac{1}{\sqrt n}\right]$
$I=\left[0,781-\dfrac{1}{\sqrt {1000}};0;781+\dfrac{1}{\sqrt {1000}}\right]$
$I\approx [0,749 ; 0,813]$
3) L’amplitude de l’intervalle de confiance est égal à $\dfrac{2}{\sqrt n}$ .
Il faut donc résoudre l’inéquation $\dfrac{2}{\sqrt n}\leq 0,02$
$\iff \sqrt n\geq \dfrac{2}{0,02}$
$\iff \sqrt n\geq 100$ (et par croissance de la fonction carré pour les nombres positifs)
$\iff n\geq 10000$
La valeur minimale de $n$ est donc $10 000$.
