Fiche de cours
Dichotomie
L'algorithme de dichotomie est une succession d'opérations permettant de donner un encadrement de la solution de l'équation $f(x) = 0$.
On cherche à savoir pour quelles valeurs une fonction $f$ s'annule, en raisonnant en tâtonnant. On choisit de manière arbitraire deux nombres $a$ et $b$ tels que $f(a) < 0$ et $f(b) > 0$.
La fonction est d'abord négative puis positive : elle passe donc par 0.
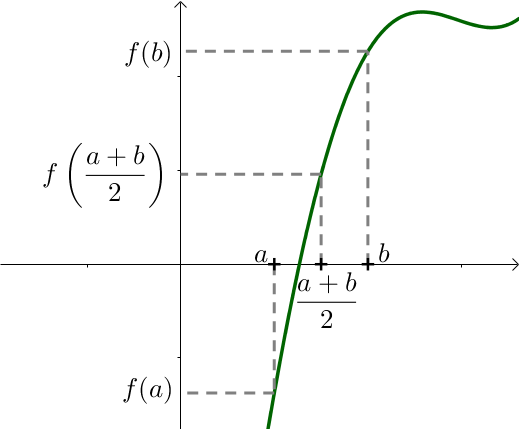
On se place ensuite au milieu de l'intervalle, c'est à dire $\dfrac{a + b}{2}$ puis on calcule l'image par la fonction $f$ de ce nouveau point que l'on compare à 0.
Ici, $f\left ( \dfrac{a + b}{2} \right ) > 0$.
On en déduit alors que la fonction s'annule dans l'intervalle $\left [a; \dfrac{a + b}{2} \right ]$.
On prend donc pour nouvelle valeur de $b$ la valeur du milieu $\dfrac{a + b}{2}$ et on conserve la même valeur pour $a$.
Puis on recommence le même procédé : on considère le milieu de l'intervalle puis on calcule l'image par la fonction $f$ de ce nouveau point.
Ici, l'image est négative, on se place donc sur la deuxième moitié de l'intervalle : le nombre $a$ change cette fois ci pour devenir $\dfrac{a + b}{2}$.
On réitère ce procédé autant de fois qu'on le souhaite pour approcher la solution à la précision désirée.
On peut alors réaliser un tableau résumant les différentes étapes de calcul de cet algorithme comprenant les valeurs de $a, b, \dfrac{a + b}{2}$ et le signe de leur image par la fonction $f$.
| Etape | 1 | 2 |
| $a$ | 1 | 1 |
| $b$ | 2 | 1,5 |
| $\dfrac{a + b}{2}$ | 1,5 | 1,25 |
| $f(a)$ | $-$ | $-$ |
| $f(b)$ | $+$ | $+$ |
| $f\left ( \dfrac{a + b}{2} \right )$ | $+$ | $-$ |
On se propose de commenter l'algorithme ci-dessous.

On indique dans un premier temps les variables utilisées dans l'algorithme.
L'entrée correspond aux valeurs que l'utilisateur doit rentrer.
$N$ correspond au nombre d'itérations de l'algorithme, c'est à dire le nombre de fois où l'on va chercher le milieu de l'intervalle et calculer son image par la fonction $f$ et étudier son signe.
Le traitement correspond à l'algorithme. $k$ compte le nombre d'itérations en cours, $m$ correspond au milieu de l'intervalle d'étude.
Enfin, on affiche les bornes de l'intervalle final qui donne un encadrement de la solution $f(x) = 0$.
