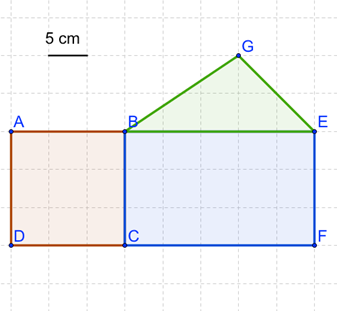
L'énoncé
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
Quelle est l'aire \(A_1\) du carré \(ABCD\) ?
\(A_1 = 15cm^2\)
\(A_1 = 25cm\)
\(A_1 = 225cm^2\)
\(A_1 = 15cm\)
Connais-tu l’aire d’un carré de coté \(c\) ?
\(A = c \times c\) (On note aussi \(A = c^2\))
Attention à l’unité.
\(A_1= 15\times 15 = 225\)
L’unité d’aire est le \(cm^2\) donc \(A_1= 225cm^2\)
Question 2
Quelle est laire \(A_2\) du rectangle \(BEFC\) ?
\(A_2= 375cm^2 \)
\(A_2= 40 cm^2\)
\(A_2= 40 cm\)
\(A_2= 375cm\)
Connais-tu l’aire d’un rectangle de dimensions \(L\) et \(l\) ?
\(A=L\times l\)
Attention à l’unité.
Le rectangle a pour dimensions \(CF = 25cm\) et \(EF = 15cm\) donc : \(A_2= 15\times 25 = 375 cm^2\)
Question 3
Dans le triangle \(BEG\), combien mesure la hauteur \(h\) issue de \(G\) ?
\(h = 2cm\)
\(h = 10cm\)
\(h = 10cm^2\)
\(h = 2cm^2\)
La hauteur passe par \(G\).
Elle est perpendiculaire au côté opposé.
Le coté opposé à \(G\) est \([BE]\).
La hauteur issue de \(G\) est le segment \( [GH]\).
\(h = GH = 10cm\)
Question 4
Quelle est l'aire \(A_3\) du triangle \(BEG\) ?
\(A_3= 250cm\)
\(A_3= 250cm^2\)
\(A_3= 15cm\)
\(A_3= 125cm^2\)
Connais-tu l’aire d’un triangle ?
\(A=b\times \dfrac{h}{2}\)
Avec \(b\) une base et \(h\) la hauteur relative à cette base.
\(A_3=\dfrac{BE \times GH}{2}=\dfrac{25\times 10}{2}= 125cm^2\)
Question 5
Quelle est l'aire \(A\) de la figure ?
\(725 cm^2\)
\(875 cm^2\)
\(750 cm\)
Autre réponse.
Les résultats ont disparu… pas de chance. Un petit effort de mémoire ?
On va t’aider :
\(A_1= 375cm^2\;; A_2= 225cm^2 ;\; A_3= 125cm^2\).
\(A_1= 375cm^2 , A_2= 225cm^2\) et \(A_3= 125cm^2\)
On sait que : \(A = A_1+A_2+A_3\)
$A = 375+225+125$
$A = 725cm^2$