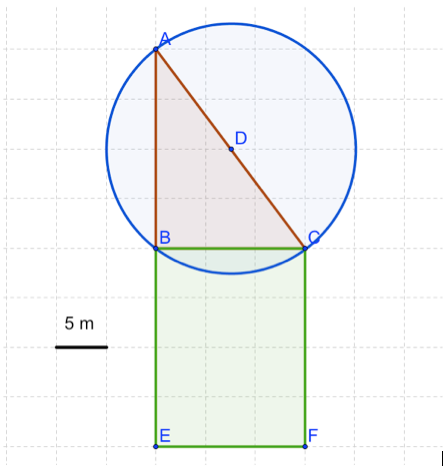
L'énoncé
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
Quelle formule donne l'aire \(A_1\) du triangle \(ABC\), rectangle en \(B\) ?
\(A_1=BC \times CA\)
\(A_1=BD \times \dfrac{AC}{2}\)
\(A_1=BC\times \dfrac{BA}{2}\)
\(A_1=BC \times BA\)
\(A = b \times \dfrac{h}{2}\)
\(B\) est une base et \(h\) la hauteur relative à cette base.
L’aire d’un triangle est donnée par :
\(A = b \times \dfrac{h}{2}\) avec \(b\) une base et \(h\) sa hauteur relative.
Ainsi :
Si \(b = BC\) alors \(h = BA\)
Et : \(A_1=BC \times \dfrac{BA}{2}\)
Question 2
On sait que : \(A_1=BC \times \dfrac{BA}{2}\). Calcule ce nombre.
\(A_1 = 60m\)
\(A_1 = 60m^2\)
\(A_1 = 150m^2\)
\(A_1 = 150cm^2\)
Attention à l’unité : ici le mètre.
\(AB = ?\) et \(AC = ?\)
\(A_1=BC \times \dfrac{BA}{2}\)
\(A_1=20\times \dfrac{15}{2}\)
\(A_1=150 m^2 \)
Question 3
Que vaut l'aire \(A_2\) du rectangle \(BCFE\) ?
\(A_2= EF \times CE\)
\(A_2= BC \times CF\)
\(A_2= 30m^2\)
\(A_2= 150m^2\)
Connais-tu bien ton cours ? C’est le moment de revoir la vidéo.
\(A = L \times l\)
\(L\) est la longueur et \(l \) la largeur.
On sait que :
\(A_2= L \times l\) avec \(L\) est la longueur et \(l \) la largeur du rectangle.
Les réponses 2 et 3 correspondent bien à cette formule.
Voyons à présent l’application numérique :
\(A_2= EF \times CF\)
\(A_2 = 15 \times 20\)
\(A_2=300 m^2\)
Question 4
On admet que le disque de diamètre \([AC]\) a pour centre \(D\) et pour rayon \(12,5 cm\).
Quelle est la formule de l'aire \(A_3\) de ce disque ?
\(A_3 = 2\pi \times (\dfrac{AC}{2})^2\)
\(A_3 = 2\pi \times (\dfrac{AC}{2})^2\)
\(A_3 = 2\pi \times AB\)
\(A_3 = \pi \times AD^2\)
Connais-tu bien ton cours ? C’est le moment de revoir la vidéo.
Cherche un rayon du disque. Il y en a plusieurs possibles sur la figure.
Attention à ne pas confondre aire et périmètre.
L’aire d’un disque est donnée par \(A = \pi \times r^2\)
\([AC]\) est un diamètre donc \(\dfrac{AC}{2}\) est un rayon.
Ici, un rayon possible est \(AD\) car \(D\) est le centre du disque.
Donc la réponse 4 est juste.
Attention à ne pas confondre avec la formule du périmètre d’un cercle.
Question 5
On choisit \(3,14\) pour valeur approchée de \(\pi\). Donne un arrondi de \(A_3\) au dixième sachant que $AD=12,5$
\(A_3 \approx 490,7 m^2\)
\(A_3 \approx 490m^2\)
\(A_3 \approx 490,6m^2\)
\(A_3 \approx 75,7m^2\)
Tu n’as qu’à remplacer par la formule.
Tu as le droit d’utiliser une calculatrice ou de poser la multiplication.
Il y a une vidéo sur les arrondis si tu ne connais pas bien. Va y faire un tour !
On utilise par exemple :
\(A_3 = \pi \times AD^2\)
\(A_3 \approx 3,14 \times 12,5^2\)
\(A_3 \approx 490,6\).