L'énoncé
Il s’agit d’un seul et même exercice. La figure est donc la même, elle est à compléter au fur et à mesure des questions.
Question 1
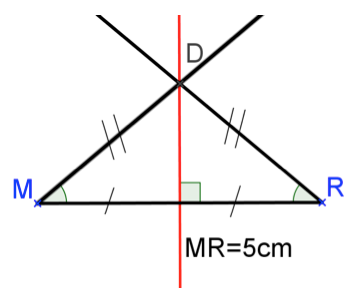
Construis un triangle \(MDR\) isocèle en \(D\) tel que \(MR=5\ cm\) et \(\widehat{DMR}= 40°\).
\(MDR\) est isocèle en \(D\) donc \(\widehat{DMR}=\widehat{DRM}=40°\).
De plus \(MR = 5\ cm\) donc tu peux tracer ce triangle.
Tu traces dabord le segment \([MR]\) de 5 cm.
Puis tu traces au rapporteur les demi-droites \([Ry)\) et \([Mx)\) telles que \(\widehat{MRy} =\widehat{RMx}=40°\).
Le point \(D\) est le point dintersection de ces deux demi-droites.
De plus \(MR = 5\ cm\) donc tu peux tracer ce triangle.
Tu traces dabord le segment \([MR]\) de 5 cm.
Puis tu traces au rapporteur les demi-droites \([Ry)\) et \([Mx)\) telles que \(\widehat{MRy} =\widehat{RMx}=40°\).
Le point \(D\) est le point dintersection de ces deux demi-droites.
\(MDR\) est isocèle en \(D\) signifie que … ?
Que \(DM=DR\) et ... ?
\(\widehat{DMR}=\widehat{DRM}=40°\) donc tu peux construire \(MDR\) !
Pense à coder la figure.
Si tu as du mal à trouver, fais une figure à main levée, cela peut t'aider à réfléchir…
Que \(DM=DR\) et ... ?
\(\widehat{DMR}=\widehat{DRM}=40°\) donc tu peux construire \(MDR\) !
Pense à coder la figure.
Si tu as du mal à trouver, fais une figure à main levée, cela peut t'aider à réfléchir…
Question 2
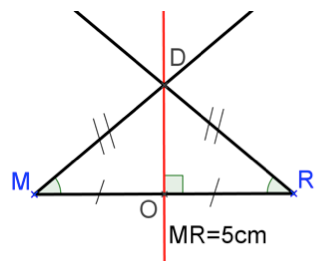
Construis en rouge le ou les axe(s) de symétrie du triangle \(MDR\) tracé dans la question précédente.
\(MDR\) est isocèle en \(D\) donc il admet un axe de symétrie : la médiatrice de la base principale \( [MR]\).
\(MDR\) est un triangle isocèle en \(D\) donc qu'admet-il ?
Un axe de symétrie qui est ... ?
La bissectrice de la base principale \([MR]\).
Un axe de symétrie qui est ... ?
La bissectrice de la base principale \([MR]\).
Question 3
Nomme \(O\) le point dintersection entre laxe rouge et \((MR)\). Que représente ce point \(O\) pour \([MR]\) ?
\(O\) est le point dintersection de \([MR]\) et de sa médiatrice donc, par définition, \(O\) est le milieu de \([MR]\).
L’axe rouge est … ?
La médiatrice de \([MR]\). Donc \(O\) est ... ?
La médiatrice de \([MR]\). Donc \(O\) est ... ?
Question 4
Quelle est la nature de \(DOR\) ? Explique pourquoi.
La droite rouge \((DO)\) est laxe de symétrie du triangle \(MDR\) isocèle en \(D\) donc \((DO)\) est la médiatrice de \([MR]\) (voir question 2).
Cela signifie, par définition, que \((DO)\) est perpendiculaire à \([MR]\) en son milieu et donc que \((DO)\) est perpendiculaire à \((MR)\) en \(O\).
Le triangle \(DOR\) a donc un angle droit, langle \(\widehat{DOR}\), donc \(DOR\) est un triangle rectangle en \(O\).
Cela signifie, par définition, que \((DO)\) est perpendiculaire à \([MR]\) en son milieu et donc que \((DO)\) est perpendiculaire à \((MR)\) en \(O\).
Le triangle \(DOR\) a donc un angle droit, langle \(\widehat{DOR}\), donc \(DOR\) est un triangle rectangle en \(O\).
Lis bien les codages de la figure.
La droite rouge est … ? Donc ?
La droite rouge est … ? Donc ?
Question 5
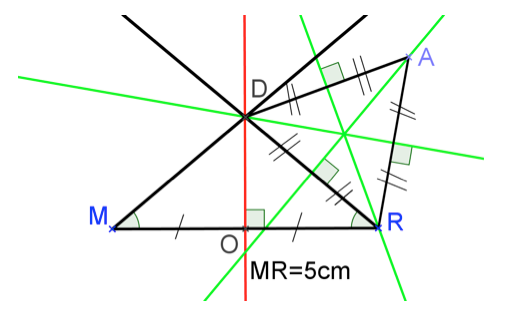
Construis un point \(A\) en dehors de \(MDR\) tel que le triangle \(DAR\) soit équilatéral. Puis construis le ou les axe(s) de symétrie de ce triangle.
Un triangle équilatéral est un triangle qui a trois côtés de même longueur.
On utilise donc le compas pour le construire. \(DAR\) est un triangle équilatéral donc ses trois angles ont la même mesure.
Si tu as retenu que cette mesure est toujours 60°, tu peux aussi tracer des angles \(\widehat{ADR}\) et \(\widehat{ARD}\) de 60° ! \(A\) sera alors le point dintersection des deux demi-droites tracées.
Et daprès le cours, un triangle équilatéral admet trois axes de symétrie : les médiatrices de ses côtés ou les bissectrices de ses angles.
On utilise donc le compas pour le construire. \(DAR\) est un triangle équilatéral donc ses trois angles ont la même mesure.
Si tu as retenu que cette mesure est toujours 60°, tu peux aussi tracer des angles \(\widehat{ADR}\) et \(\widehat{ARD}\) de 60° ! \(A\) sera alors le point dintersection des deux demi-droites tracées.
Et daprès le cours, un triangle équilatéral admet trois axes de symétrie : les médiatrices de ses côtés ou les bissectrices de ses angles.
Qu’est-ce qu’un triangle équilatéral ?
Un triangle équilatéral est un triangle qui a trois côtés de même longueur.
Des longueurs égales, on utilise donc le … ?
Compas !
Un triangle équilatéral est un triangle qui a trois côtés de même longueur.
Des longueurs égales, on utilise donc le … ?
Compas !