L'énoncé
Cet exercice est un QCM. Coche la ou les bonne(s) réponse(s).
Tu as obtenu le score de
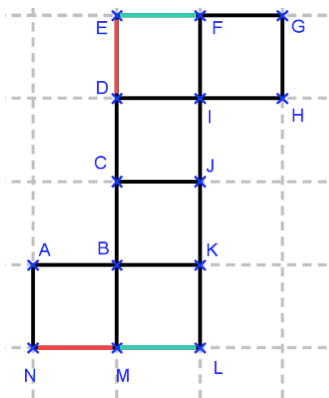
Question 1
La figure ci-dessous :
Est le patron d’un pavé droit.
Est le patron d’un cube.
N’est pas le patron d’un pavé.
Ne permet pas de construire un solide.
Compte le nombre de faces.
Utilise les carreaux pour vérifier les arêtes de même longueur et les faces identiques.
Essaie de visualiser la construction d’un pavé ou d’un cube.
Un cube est un pavé droit particulier donc, si on répond la deuxième proposition, on doit aussi répondre la première.
Question 2
Cite deux segments de ce patron qui se superposent (ou se touchent) lorsqu'on construit le cube.
[JK] et [FI].
[ED] et [MN].
[KL] et [GH].
[EF] et [ML].
Imagine le découpage et le pliage pour visualiser les segments qui se superposent et forment une arête du cube.
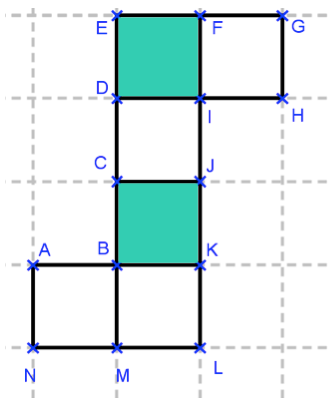
Question 3
Cite deux faces qui seront opposées dans le cube construit.
CJKB et FGHI.
CJKB et ABMN.
CJKB et DEFI.
BKLM et DEFI.
Deux faces opposées ne peuvent être « collées » dans le patron.
Deux faces opposées sont superposables, elles ont les mêmes dimensions.
Imagine le découpage et le pliage pour visualiser les faces opposées.
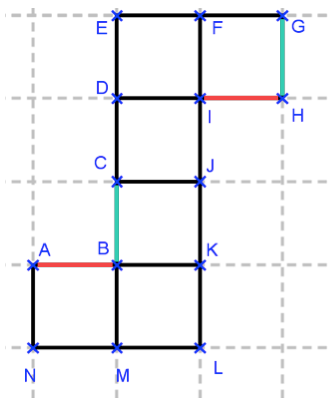
Question 4
Cite deux segments du patron qui donneront deux arrêtes parallèles du cube.
[AB] et [IH].
[ED] et [IJ].
[JK] et [IJ].
[CB] et [GH].
Toutes les arêtes parallèles d’un pavé droit sont de même longueur.
Question 5
Cite les segments du patron qui donneront deux arêtes perpendiculaires du cube.
[AB] et [BC].
[AB] et [BK].
[IJ] et [GH].
[MN] et [EF].
Tu peux procéder par élimination.
Essaie de visualiser la construction du cube.
