L'énoncé
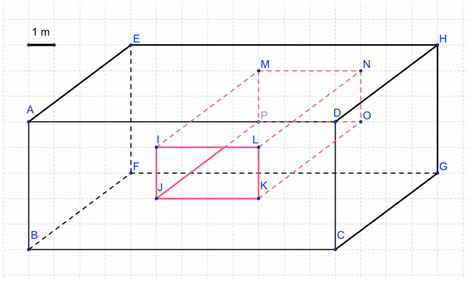
Un bloc de béton (pavé noir) est utilisé pour supporter un pont. Une partie creuse, représentée en rouge, est utilisée pour faire passer différents câbles électriques. Les ingénieurs souhaitent connaître le volume de béton nécessaire à la construction de ce pilier.
On admet que \(AE = 6\mbox{ m}\)
Question 1
Quel est le volume \(V_1\) du pavé \(ABCDEFGH\) ?
On a :
\(\begin{align*} & V_1 = BC \times AB \times AE \\
& V_1 = 12 \times 5 \times 6 \\ & V_1 = 360\mbox{ m}^3 \end{align*}\)
Connais-tu bien la formule ?
\(V = L \times l \times h\)
Question 2
Quel est le volume \(V_2\) du pavé \(IJKLMPON\) ?
On a :
\(\begin{align*} & V_2 = IJ \times IL \times IM \\
& V_2 = 2\times4\times6 \\
& V_2 = 48\mbox{ m}^3 \end{align*}\)
Connais-tu bien la formule ?
\( V = L\times l \times h\)
Question 3
Quel volume \(V_3\) de béton faudra t-il prévoir ?
On a : \(V_3 = V_1-V_2\) car le volume de béton est celui du volume du grand pavé auquel on enlève le volume du pavé sans béton.
\(\begin{align*} &V_3 = V_1-V_2 \\ & V_3 = 360-48 \\ & V_3 = 312\mbox{ m}^3 \end{align*}\)
Exprime \(V_3\) en fonction de \(V_1\) et de \(V_2\).
\( V_3 = ?\)
\(V_3 = V_1-V_2\) bien sûr !
Question 4
Observe bien ce tableau : il représente la répartition des matériaux pour réaliser \(1\mbox{ m}^3\) de béton.
| Ciment | Sable | Graviers | Eau |
| 350 Kg | 400 Kg | 800 Kg | 90 L |
Quel volume \(V_{eau}\) d'eau devra t-on prévoir pour réaliser ce pilier ? Donne ce nombre en \(\mbox{m}^3\).
On a :
\(\begin{align*} & V_{eau} = 90 \times 312 \\ & V_{eau} = 28 080\mbox{ L}\end{align*}\)
Soit :
\(V_{eau} = 28,08\mbox{ m}^3\)
Tu connais le nombre de \(\mbox{m}^3\) de béton.
Il s’agit donc de multiplier deux nombres.
Question 5
Quelle masse \(M \)de sable et graviers faudra t-il alors prévoir ? Donne ce résultat en tonnes.
On a :
\(\begin{align*} & M = (400+800) \times 312 \\ & M = 1200 \times 312 \\ & M = 374400\mbox{ Kg} \\ & M = 374,4\mbox{ t} \end{align*}\)
Pense à additionner les masses de sable et de graviers.
N’oublie pas qu’il y a \(312\mbox{ m}^3\) de béton.
Rappelle-toi enfin que \(1\mbox{ t} = 1000\mbox{ Kg}\).
