L'énoncé
On utilisera dans cet exercice le logiciel Algobox, gratuit et téléchargeable sur internet. Il existe d'autres logiciels d'algorithmique bien entendu. Lesbonsprofs n'ont pas de préférence.
On considère l’algorithme suivant :
VARIABLES :
\(x\) EST_DU_TYPE NOMBRE
\(a\) EST_DU_TYPE NOMBRE
\(b\) EST_DU_TYPE NOMBRE
\(c\) EST_DU_TYPE NOMBRE
DEBUT_ALGORITHME
LIRE \(x\)
\(a\) PREND_LA_VALEUR \(x^2\)
\(b\) PREND_LA_VALEUR \(2 \times x\)
\(c\) PREND_LA_VALEUR \(a-4 \times b +16\)
AFFICHER \(c\)
FIN_ALGORITHME
Question 1
Déterminez les images des réels $2, 4$ et $-2$ par l'algorithme.
L'image de $2$ vaut $4$.
L'image de $4$ vaut $0$.
L'image de $-2$ vaut $36$.
La fonction \(pow(x,n)\) signifie \(x^n\).
Suivez bien l’enchainement des calculs.
On vous recommande de télécharger Algobox, de recopier cet algorithme et de le tester véritablement. C’est la meilleure façon de bien connaître ces notions.
Question 2
On appelle \(f\) la fonction associée à l'algorithme précédent. Déterminez l'expression algébrique de \(f\) en fonction de la variable réelle \(x\).
\(f(x) = x^2-8x+16\)
Les valeurs de \(a\) et \(b\) sont connues.
On peut conclure.
Question 3
Montrez que tous les résultats de l'algorithme sont des carrés.
\(f(x) = (x-4)^2\)
Ne voyez vous pas une égalité remarquable ici ?
On a bien : \(a^2-2ab+b^2\)...
Question 4
Pour quelles valeurs de la variable \(x\) l'algorithme donne-t-il $16$ comme résultat ?
\(f(x) = 16\) signifie que \(x^2-8x+16 = 16\).
Soit \(x^2-8x = 0\).
On factorise par \(x : x(x-8) = 0\). Ce produit est nul si et seulement si \(x = 0\) ou \(x = 8\).
\(S = \{0 ; 8\}\)
On va donc chercher à résoudre \(f(x) = 16\).
Cela revient à chercher les antécédents de 16.
Question 5
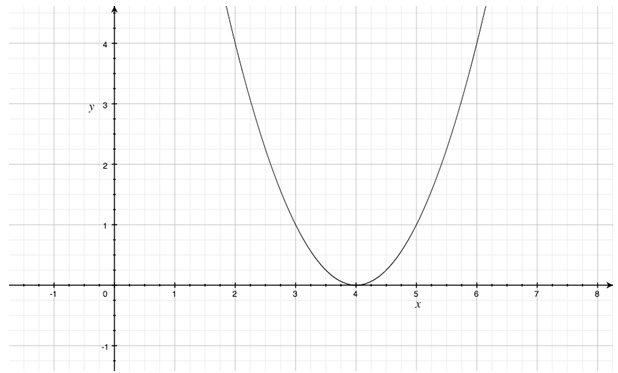
\(f(x)\) semble avoir un minimum. Que vaut-il et quand est-il atteint ?
\(f(x) = 0\), lorsque \(x-4 = 0\) c'est à dire lorsque \(x = 4\).
L'image de $4$ vaut $0$. Le minimum de \(f\) est donc le nombre $0$. Il est atteint lorsque \(x = 4\).
Graphiquement, cela correspond au point \(T(4 ; 0)\).
Voici pour information la représentation graphique de la fonction \(f(x)\).
Quelle est la plus petite valeur prise par un carré ?
\(f(x)\) est sous la forme d’un carré donc sa valeur minimale est 0.
\((x-4)^2= 0\) lorsque \(x-4 = 0\). Cela nous indique la valeur de \(x\) pour laquelle \(f\) est minimale.