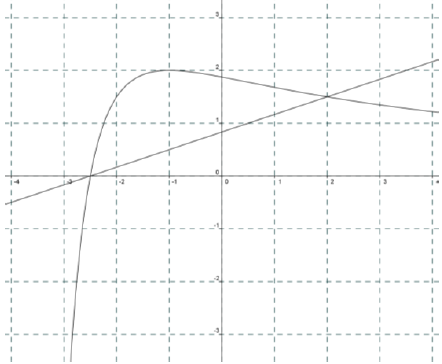
La courbe (C) est la représentation d’une fonction $f$ définie sur $]-4 ;4]$ et la droite (D) est la représentation d’une fonction affine $g$.
Tous les résultats de lecture graphique seront donnés à $0,1$ près.
1) Lire $f(-1)$ et $f(2)$
2) Lire les antécédents de $1$ et $1,5$ par $f$.
3) Dresser le tableau de variations de $f$.
4) Résoudre graphiquement dans l’intervalle $]-4 ;4]$
a) Les équations $f(x) =0$ et $f(x) = g(x)$
b) Les inéquations $f(x) >0$ et $f(x) \leq g(x)$
Exercice :
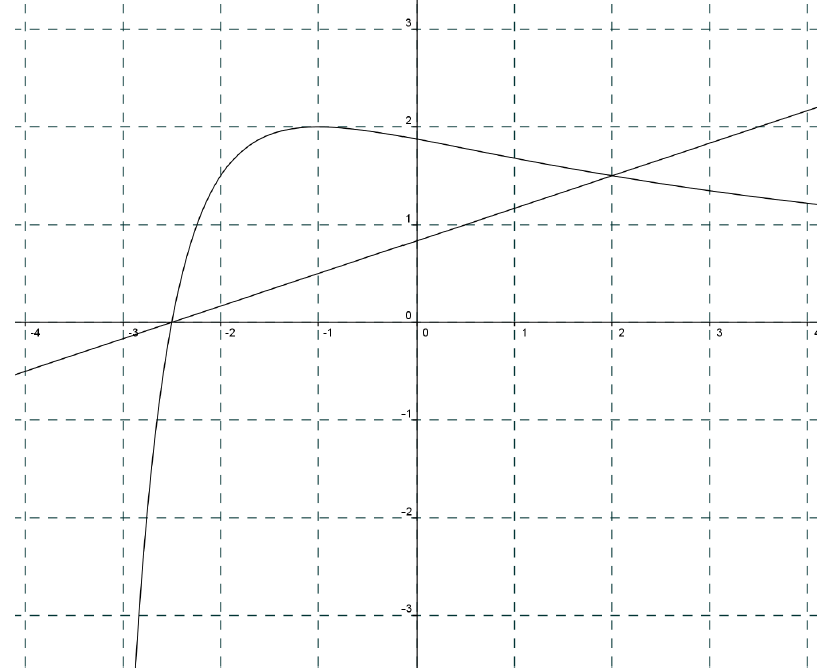
La courbe (C) est la représentation graphique d’une fonction $f$ définie sur $]-4 ;4]$ et la droite (D) est la représentation d’une fonction affine $g$.
1) $f(-1)=2$ et $f(2) \approx 1,5$.
2) l’antécédent de $1$ est $-2,25$ et les antécédents de $1,5$ sont $-2$ et $2$
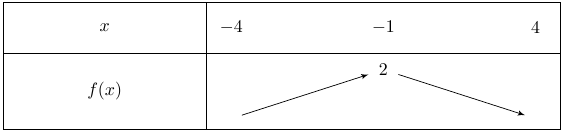
3)
4) a) l’équation $f(x)=0$ a pour solution $-2,5$
l’équation et $f(x)=g(x)$ a pour solutions $-2,5$ et $2$.
b) l’inéquation $f(x) >0$ a pour ensemble de solutions $]-2,5 ;4]$
L’inéquation $f(x) \leq g(x)$ a pour ensemble de solutions $]-4 ;-2,5] \cup [2 ;4]$
