Fiche de cours
Résolutions graphiques d'équations
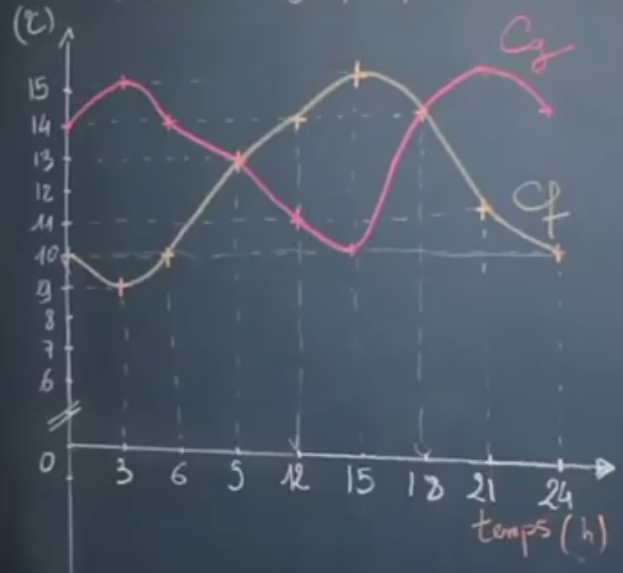
Considérons deux fonctions $f$ et $g$ représentant la température au cours du temps dans deux villes différentes.
Equations du type $f(t)=k$ avec $k\in \mathbb{R}$
Résoudre l'équation $f(t) = 14$ revient à chercher les antécédents de 14 par la fonction $f$.
Pour se faire, on se place sur l'axe des ordonnées(l'axe des températures ici) et on trace la droite perpendiculaire à cet axe puis on regarde les points d'intersection entre la droite et la courbe de température et finalement, on lit leur abscisse.
Ici, il y a deux points d'intersections pour lesquels la température est de 14°C et donc deux heures différentes : 12h et 18h. Ainsi $S = \{12; 18\}$.
Résoudre l'équation $f(t) = 8$ revient à chercher les antécédents de 8 par la fonction $f$.
Or il ne fait jamais 8°C, c'est à dire que la droite perpendiculaire à l'axe des ordonnées passant par $y = 14$ ne coupe jamais la courbe de $f$.
Ainsi $S = \varnothing$ et dans
