L'énoncé
Soit \(f\) la fonction définie sur \([-4 \ ; 2]\) par \(f(x) = -2x^2-4x\)
On notera \(C_f\) la représentation graphique de \(f\) dans un repère orthogonal.
Question 1
Factorisez au maximum \(f(x).\)
\(f(x) = -2x(x+2)\)
Il y a un facteur commun évident.
Le nombre \(-2x\) bien sur.
Question 2
Résolvez \(f(x) =0.\)
En déduire les coordonnées des points intersections de \(C_f\) avec l'axe des abscisses.
\(f(x) =0\) équivaut à :
\(-2x(x+2)=0\)
Ce produit de facteurs est nul si et seulement si l'un au moins des facteurs est nul.
\(-2x = 0 \ ou \ x+2 = 0\)
\(x=0 \ ou \ x=-2\)
Ainsi les solutions sont :
\(S=\{-2 \ ;0\}\)
Les coordonnées des points cherchés sont donc \(A(-2 \ ; 0) \ et \ O(0 \ ; 0). \)
Utilisez l’expression factorisée de \(f(x).\)
Il s’agit d’une équation produit nul. Savez-vous les résoudre ?
Il y a une vidéo sur le site dans le chapitre « équations et inéquations ».
Question 3
Montrez que pour tout réel \(x\) de \([-4 \ ; 2]\)
\( f(x) = -2(x+1)^2+2\)
\(f(x) = -2x^2-4x\)
\(f(x) = -2(x^2+2x) \)
On note que \(x^2+2x\) est le début de l'égalité remarquable \((x+1)^2=x^2+2x+1\)
\(f(x) =-2(x^2+2x+1-1)\)
\(f(x)= -2(x^2+2x+1) +2\)
\(f(x) = -2(x+1)^2+2\)
Vous avez trouvé ici la forme canonique de \(f\).
Partez de l’expression \(f(x) = -2x^2-4x\) et factorisez par \(-2\).
Le terme \(x^2+2x\) est le début d’une égalité remarquable. Laquelle ?
Équilibrez à présent votre expression pour avoir une expression égale à \(f(x).\)
Question 4
Conjecturez à l'aide de la calculatrice le maximum de \(f \ sur \ [-4 \ ; 2].\)
(C'est-à-dire essayez de le deviner sans le démontrer en traçant la courbe \(C_f\) sur votre calculatrice graphique. On pourra aussi observer le tableau de valeurs de votre fonction.)
Le maximum de la fonction semble être, d'après la calculatrice, proche de 2.
Une conjecture n’est pas une preuve. C’est une hypothèse que l’on formule.
Vous devez rédiger en disant : « Il semblerait que… » ou « Le maximum pourrait être… ».
Question 5
Pour quelle valeur ce maximum semble-t-il atteint ?
D'après la calculatrice, le maximum semble atteint lorsque \(x = -1.\)
Attention, on ne cherche pas de valeur approchée du maximum dans cette question.
On cherche la valeur approchée de \(x\) pour laquelle la fonction admet un maximum.
Question 6
Démontrez les conjectures faites aux questions 3 et 4 par le calcul.
En bref, prouvez que le maximum de \(f\) est \(2\) et qu'il est atteint en \(x=-1\).
On sait que \(f(x) = -2(x+1)^2+2\)
C'est-à-dire \(f(x) = -2(x-(-1))^2+2\)
Si on veut que cela ressemble exactement à l'expression donnée dans le cours.
On en déduit que le sommet de la parabole a pour coordonnées \(S(-1 ;2).\)
Le nombre coefficient devant \((x+1)^2\) est \(-2.\)
Cest un nombre négatif donc les branches de la parabole sont dirigées vers les ordonnées négatives.
Il résulte de cela que le sommet \(S\) est associé au maximum de la fonction.
Conclusion : Le maximum de \(f\) vaut \(2\). Il est atteint en \(x = -1.\)
C’est le moment d’utiliser le cours sur le second degré. Regardez la vidéo dans les prérequis si besoin.
Rappelez-vous : Si \(f(x) = a(x -\alpha)^2 + \beta\) alors le sommet de la parabole \(C_f\) est \(S(\alpha \ ;\beta)\)
La parabole peut avoir les branches dirigées vers les ordonnées positives ou vers les ordonnées négatives. Savez-vous à quelle condition ?
Cela dépend du signe de \(a\). Ici, \(a=-2.\)
Question 7
Imprimez ou recopiez ce tableau de valeurs et complétez-le. (On donnera les valeurs exactes.)
Vous pouvez bien sûr utiliser le tableau de valeurs de votre calculatrice.
| x | -4 | -3,5 | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
| f(x) |
| x | -4 | -3,5 | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
| f(x) | -16 | -10.5 | -6 | -2.5 | 0 | 1.5 | 2 | 1.5 | 0 | -2.5 | -6 | -10.5 | -16 |
On connait déjà les images de \(-2 \ et \ 0.\)
Pour le reste, utilisez votre calculatrice ou lancez-vous dans un grand moment de calcul mental.
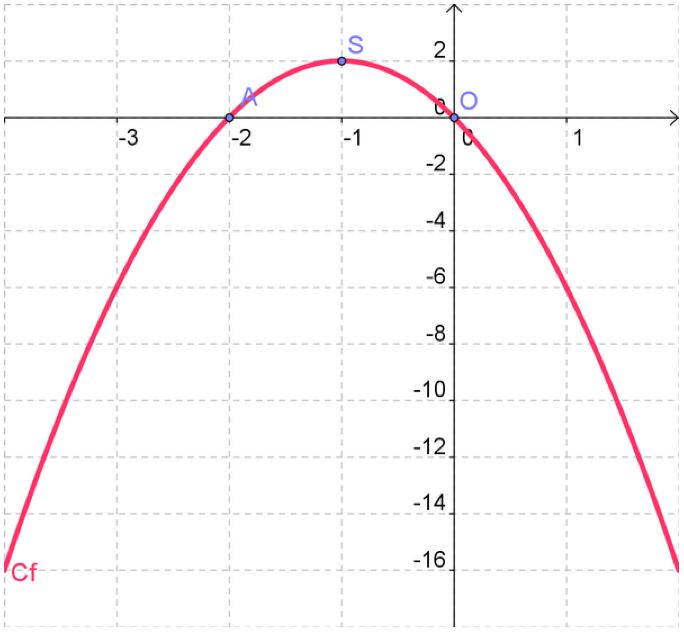
Question 8
Tracez \(C_f,\) la courbe représentative de la fonction \(f\) dans un repère orthogonal.
Là encore la calculatrice peut s’avérer utile.
Réfléchissez bien aux unités que vous allez choisir sur les axes.
Vous n’êtes pas obligé de choisir la même unité sur les deux axes.
Placez en premier le sommet de la parabole.