L'énoncé
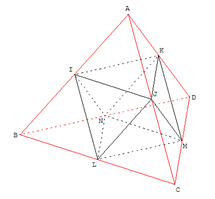
Soit \(ABCD\) un tétraèdre régulier d’arête égale à 10 cm. Les points \(I\), \(J\), \(K\), \(L\), \(M\) et \(N\) sont les milieux des arêtes du tétraèdre. L’objectif est de calculer le volume et l’aire latérale du solide \(IJKLMN\).
Tu as obtenu le score de
Question 1
Comparez la longueur \(IJ\) et la longueur \(BC\).
\(IJ = BC\)
\(IJ = \dfrac{BC}{2}\)
\(IJ = 2BC\)
Aucune des réponses précédentes n’est exacte.
Connaissez-vous la propriété de la droite des milieux ?
Question 2
On observe à présent le solide \(IJLMNK\). Sachant que toutes les arêtes ont la même longueur et que ses faces sont des triangles équilatéraux, Comment se nomme t-il ?
Un icosaèdre régulier.
Un dodécaèdre régulier.
Un octaèdre régulier.
Aucune des réponses précédentes n’est exacte.
Comptez le nombre de faces identiques.
Comment nomme-t-on un homme âgé de 80 ans ?
Un octogénaire…
Question 3
Calculez l'aire \(A_{BCD}\) de la base du tétraèdre.
\(A_{BCD} = 50\sqrt{5} cm^2\)
\(A_{BCD} = 5\sqrt{3} cm^2\)
\(A_{BCD} = 25\sqrt{3} cm^2\)
Aucune des réponses précédentes n’est exacte.
Il y a plusieurs étapes de calcul. Commencez par chercher la longueur \(BM\) par exemple.
Il y a un joli triangle rectangle car médianes et médiatrices sont confondues dans un triangle équilatéral.
Vous pouvez à présent calculer l’aire du triangle équilatéral en choisissant \(CD\) comme longueur de base.
Question 4
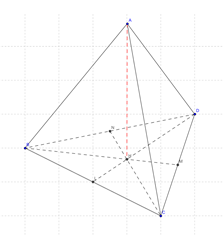
On s'intéresse à la figure suivante, sans la représentation de loctaèdre \(IJKLMN\).
On note \(H\) le pied de la hauteur du tétraèdre. Calculez \(BH\).
\(BH = \dfrac{1}{2} \times BM = \dfrac{5}{2}\sqrt{3} cm\)
\(BH = \dfrac{1}{3} \times BM = \dfrac{5}{3}\sqrt{3} cm\)
\(BH = \dfrac{2}{3} \times BM = \dfrac{10}{3}\sqrt{3} cm\)
Aucune des réponses précédentes n’est exacte.
\(H\) est le point de concours des médianes de \(ABD\).
Savez-vous quelle est la position du centre de gravité d’un triangle sur chacune de ses médianes ?
Vous pouvez revoir la vidéo sur les droites remarquables.
Question 5
\(AH = 10\sqrt{\dfrac{2}{3}} cm\)
\(AH = 100\sqrt{\dfrac{2}{3}} cm\)
\(AH = 10\sqrt{\dfrac{5}{3}} cm\)
Aucune des réponses précédentes n’est exacte.
Le triangle \(ABH\) est rectangle en \(H\).
Question 6
Sachant que \(A_{BCD} = 25\sqrt{3} cm^2\) et que la hauteur \(AH\) vaut \(10\sqrt{\dfrac{2}{3}}\) cm, calculez le volume \(V\) du tétraèdre.
\(V = \dfrac{250}{3} \times \sqrt{3} cm^3\)
\(V = \dfrac{125}{3} \times \sqrt{2} cm^3\)
\(V = \dfrac{250}{3} \times \sqrt{2} cm^3\)
Aucune des réponses précédentes n’est exacte.
Connaissez-vous la formule du volume d’une pyramide ? C’est dans votre cours.
Un tétraèdre est en effet, une pyramide à base triangulaire.
Question 7
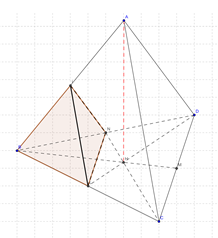
On remarque que le volume de l'octaèdre \(IJKLMN\) est celui du tétraèdre \(ABCD\) auquel on enlève quatre volumes identiques de quatre plus petits tétraèdres.
On en a représenté un ici : le tétraèdre \(LINB\). Quel est son volume \(V\) ?
\(V’ = \dfrac{1}{8} \times V = \dfrac{125}{12} \times \sqrt{2} cm^3\)
\(V’ = \dfrac{1}{4} \times V = \dfrac{125}{6} \times \sqrt{2} cm^3\)
\(V’ = \dfrac{1}{2} \times V = \dfrac{125}{3} \times \sqrt{2} cm^3\)
Aucune des réponses précédentes n’est exacte.
Par quel facteur a-t-on multiplié les dimensions de \(ABCD\) pour obtenir celle de \(LINB\) ?
Par \(\dfrac{1}{2}\) bien sûr.
Comment trouver \(V’\) astucieusement sachant cela et connaissant \(V\) le volume du tétraèdre \(ABCD\) ?
Question 8
Sachant que \(A_{BCD} = 25\sqrt{3} cm^2\)
Calculez l'aire latérale \(A_1\) de l'octaèdre \(IJKLMN\).
\(A_1=50\sqrt{3} cm^2\)
\(A_1=25\sqrt{3} cm^2\)
\(A_1=125\sqrt{3} cm^2\)
Aucune des réponses précédentes n’est exacte.
Commencez par calculer l’aire d’une de ses faces. Il y en a 8 !
On connaît l’aire de \(BCD\) et les dimensions sont deux fois plus petites.
Donc l’aire est…
Quatre fois plus petite.
Question 9
\(V = \dfrac{250}{3} \times \sqrt{2} cm^3\)
\(V = \dfrac{125}{12} \times \sqrt{2} cm^3\)
Calculez le volume \(V_1\) de l'octaèdre \(IJKLMN\).
\(V_1=V-4V'= \dfrac{125}{3} \times \sqrt{2} cm^3\)
\(V_1=V-4V'= 250 \times \sqrt{2} cm^3\)
\(V_1=V-4V'= \dfrac{250}{3} \times \sqrt{2} cm^3\)
Aucune des réponses précédentes n’est exacte.
On ne travaille qu’avec des valeurs exactes.
Il y a quatre petits tétraèdres comme \(LINB\).
Question 10
\(V = \dfrac{125}{12} \times \sqrt{2} cm^3\)
\(V_1=V-4V'= \dfrac{125}{3} \times \sqrt{2} cm^3\)
Supposons que l'arête de \(ABCD\) ait mesuré 2 cm. Quel aurait été le volume de l'octaèdre ?
\(V_1=5 \dfrac{\sqrt{2}}{3} cm^3\)
\(V_1= 25 \dfrac{\sqrt{2}}{3} cm^3\)
\(V_1= \dfrac{\sqrt{2}}{3} cm^3\)
Aucune des réponses précédentes n’est exacte.
Si les dimensions sont multipliées par \(\dfrac{1}{5}\), alors le volume est multiplié par…
Le cube de \(\dfrac{1}{5}\).