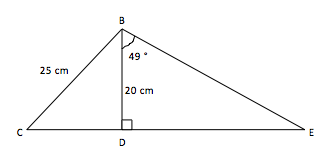
L'énoncé
On considère la figure suivante où les points C, D et E sont alignés.
Tu as obtenu le score de
Question 1
La figure n'est pas à l'échelle. On désire calculer la valeur exacte de la distance \(CD\).
Quelle règle devez-vous utiliser ici ?
Les règles de la trigonométrie.
Le théorème de Pythagore.
Le théorème de Thalès.
La réciproque du théorème de Pythagore.
Le côté \([CD]\) est un côté d’un triangle rectangle...
Dont on connait les longueurs des deux autres côtés.
Question 2
Il faut donc utiliser le théorème de Pythagore dans le triangle rectangle \(BCD\).
D'après ce théorème, quelle relation entre les trois côtés du triangle pouvez-vous écrire ?
\(BD^2 = CD^2 + BC^2\)
\(CD^2 = BC^2 + BD^2\)
\(BC^2 = CD^2 + BD^2\)
\(BC = CD + BD\)
Le carré de l’hypoténuse…
Est égal à la somme des carrés des deux autres côtés.
Question 3
On a donc \(BC^2 = CD^2 + BD^2\), quelle relation obtiendrez-vous si vous remplacez par les valeurs de l'énoncé ?
\(50 = CD^2 + 40\)
\(625 = CD^2 + 400\)
\(25 = CD^2 + 20\)
\(625 = CD + 400\)
Pas trop dure cette étape !
\(25^2 = 25 \times 25 \) et \( 20^2 = 20 \times 20\)
Question 4
Puisque \(625 = CD^2 + 400\), quelle est la valeur de \(CD^2\) ?
\(CD^2 = 625 - 400 = 225\)
\(CD^2 = 625 + 400 = 1025\)
\(CD^2 = 400 - 625 = -225\)
\(CD^2 = \frac{625}{400} = 1,5624\)
Pour isoler \(CD^2\), il suffit que tu soustraies 400 de chaque membre de l’égalité.
Question 5
\(CD^2\) est donc égal à 225, quelle est la valeur exacte de \(CD\) ?
\(CD = \sqrt{225} = 112,5\)
\(CD = \sqrt{225} = 50 625\)
\(CD = \sqrt{225} = 225\)
\(CD = \sqrt{225} = 15\)
\(\sqrt{225}\) est le nombre positif, qui mis au carré, donne 225.
Question 6
On veut calculer maintenant l'arrondi de la distance \(DE\) au millimètre près.
Quelle règle devez-vous utiliser ici ?
Le cosinus de l’angle $49°$
Le sinus de l’angle $49°$
La tangente de l’angle $49°$
Le théorème de Pythagore
Dans le triangle \(BDE\), pour l’angle \(\widehat{BDE} \) je connais \(BD\) et je recherche \(DE\).
\([BD]\) est le côté adjacent et \([DE]\) est le côté opposé.
Question 7
À combien est égale la tangente de l'angle $49°$ ?
\(\tan (49°)=\dfrac{BD}{DE}\)
\(\tan (49°) =\dfrac{DE}{BD}\)
\(\tan (49°)=\dfrac{DE}{BE}\)
\(\tan (49°)=\dfrac{BD}{DE}\)
Vous connaissez CAH-SOH-TOA ?
Cosinus Adjacent Hypoténuse – Sinus Opposé Hypoténuse – Tangente Opposé Adjacent
C’est un moyen mnémotechnique pour se souvenir des cosinus, sinus et tangente,
Par exemple, tangente = \( \large\frac{côté \ opposé}{côté adjacent}\)
Question 8
On a donc \(\tan (49°) =\dfrac{DE}{BD'}\) ce qui donne \(\tan (49°) = \dfrac{DE}{20}\).
Que vaut \(DE\) ?
\(DE = \dfrac{20}{\tan(49°)}\)
\(DE = \tan (49 \times 20)\)
\(DE = \dfrac{\tan(49°)}{20}\)
\(DE = 20 \times \tan (49°)\)
Pour isoler \(DE\), multipliez chaque membre par $20$.
Question 9
\(DE = 20 \times \tan (49°)\)
Que vaut l'arrondi de la distance \(DE\) au millimètre près ?
\(DE = 63,5\) cm.
\(DE = 23,0\) cm.
\(DE = 1776,6\) cm.
\(DE = 23,007 \) cm.
Le résultat est exprimé en cm.
Pour arrondir au millimètre près, il faut donc arrondir au dixième.
Question 10
Pour terminer, en déduire l'arrondi de la distance \(CE\) au millimètre près.
\(CE = 38\)
\(CE \approx 38\)
\(CE \approx 38,007\)
\(CE = 38,007\)
Depuis la question 5, on sait que \(CD = 15\) cm.
Et depuis la question 9, on sait que \(DE \approx 23,0\) cm.