L'énoncé
Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
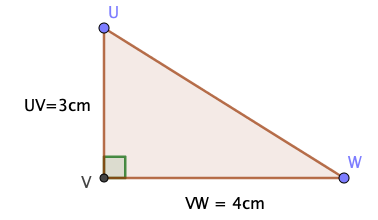
Citer la propriété de Pythagore dans ce triangle.
$UW^2+UV^2=VW^2$
$VW^2+UV^2=UW^2$
$UW+UV=VW$
$UV^2-UW^2=VW^2$
C'est une question de cours.
Il faut repérer l'hypoténuse : $[UW]$ dans le triangle rectangle $UVW.$
Ainsi le théorème de Pythagore nous donne :
$VW^2+UV^2=UW^2$
Question 2
Calculer $UW$

$25$
$7$
$5$
$1$
Il suffit d'appliquer le théorème.
On a : $VW^2+UV^2=UW^2$
$4^2+3^2 = UW^2$
$16+9=UW^2$
$25=UW^2$
$\sqrt{25}=UW$
Finalement, $UW=5$
Question 3

Si on double les longueurs de $[UV]$ et de$[VW]$ alors la longueur de $[UW]$ sera multipliée par :
$2^2=4$
$\sqrt2$
$2$
$1$
Il s'agit d'un agrandissement de facteur $2$.
Chaque longueur sera donc multiplié par $2$.
Si on avait cherché l'aire de la nouvelle figure, on aurait multiplié l'ancienne par $4$.
Question 4
Citer la propriété de Pythagore dans une triangle $SKI$, rectangle en $K$
$SI^2+SK^2=IK^2$
$SI^2=SK^2+IK^2$
$SI^2= SK^2-IK^2$
Question 5
Citer la propriété de Pythagore dans une triangle $FOU$, rectangle en $U$
$FO^2=UF^2+OU^2$
$[FO]$ est l'hypoténuse puisque le triangle est rectangle en $U$
$FO^2=UF^2-OU^2$
$FO^2+UF^2=OU^2$

$[SI]$ est l'hypoténuse puisque le triangle est rectangle en $K$