L'énoncé
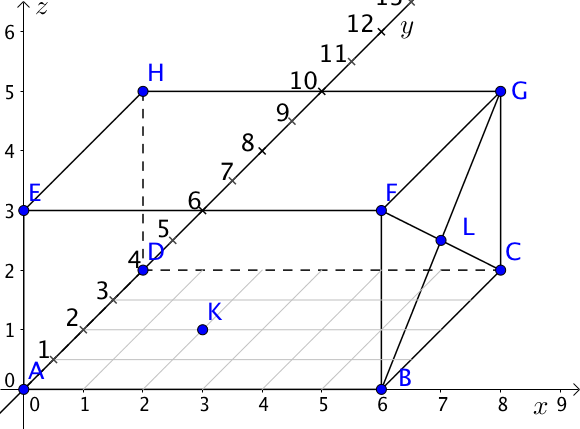
Dans tout l'exercice, on utilisera la figure suivante :
$[Ox)$ est l'axe des abscisses, $[Oy)$ l'axe des ordonnées et $[Oz)$ l'axe des altitudes.
Question 1
Quelles sont les coordonnées du point $F$ ?
Le point $F$ appartient à la face $ABFE$, il n'a donc pas de composante selon l'axe des ordonnées.
On lit ainsi que $F$ a une abscisse de 6 et une altitude de 3.
Ainsi on a le résultat suivant $F(6; 0; 3)$.
Question 2
Quelles sont les coordonnées du point $H$ ?
Le point $H$ appartient à la face $ADHE$, son abscisse est donc celle de $E$ c'est à dire $0$.
Graphiquement, on trouve alors $H(0; 4; 3)$.
Question 3
Quelles sont les coordonnées du point $G$ ?
Le point $G$ appartient à la face $BCGF$. Son abscisse est donc 6.
Pour atteindre $G$ depuis cette face, il faut se déplacer de 4 unités dans la direction des ordonnées puis monter de 3 dans la direction de l'altitude.
Ainsi, $G(6; 4; 3)$.
Question 4
Quelles sont les coordonnées du point $L$ ?
$L$ appartient à la face $BCGF$, il a donc pour abscisse 6.
$L$ se situe de plus à l'intersection des diagonales. Or $BCGF$ est un rectangle de longueur 4 et de largeur 3.
Il en résulte que l'ordonnée et l'altitude de $L$ correspondent à la moitié de la longueur et de la largeur.
Ainsi, $L \left(6; 2; \dfrac{3}{2} \right )$
$L$ est le point d'intersection des diagonales de la face $BCGF$
Question 5
En sachant que le point $K$ appartient à la face $ABCD$, donner les coordonnées de ce point.
Pour lire l'abscisse de ce point, on trace la droite parallèle à l'axe des ordonnées pesant par $K$. L'abscisse est alors lue au point d'intersection de cette droite avec l'axe des abscisses, c'est à dire 2.
De même, on trace la droite parallèle à l'axe des abscisses passant par ce point. L'ordonnée est alors lue au point d'intersection de cette droite avec l'axe des ordonnées, c'est à dire 2.
En outre, le point $K$ n'a pas d'altitude.
Les coordonnées sont donc $K(2; 2; 0)$.
