L'énoncé
Les voitures électriques deviennent des nouveaux acteurs du transport en représentant une alternative à l’utilisation des énergies fossiles. Elles présentent l’avantage de ne pas émettre de dioxyde de carbone lors de leur utilisation. L’achat de véhicules électriques ne cesse d’augmenter ces dernières années.
L’objectif de cet exercice est d’étudier la charge de la batterie d’un véhicule électrique à partir d’une borne de recharge et sa décharge lors de la circulation du véhicule sur une autoroute.
1. Étude de la charge du véhicule électrique avec une borne de recharge
Le propriétaire d’une voiture électrique veut charger la batterie de son véhicule alors que la jauge d’autonomie de la batterie indique 20 %. Pour cela il utilise une borne de recharge fournissant une puissance constante de 7,40 kW en délivrant un courant électrique d’intensité constante de 32,0 A.
Les batteries lithium-ion
Les batteries utilisées couramment dans les véhicules électriques, mais également dans d’autres applications comme les téléphones portables, sont de type lithium-ion. Elles présentent l’avantage d’une très grande énergie massique comprise entre 90 Wh·kg-1 et 180 Wh·kg-1. De plus, ces batteries, même partiellement déchargées, délivrent toujours la même puissance, permettant une utilisation dans les mêmes conditions quel que soit le niveau de charge.

Des cellules constitutives d’une batterie d’un véhicule électrique de 41 kWh
Quelques caractéristiques du véhicule électrique étudié
|
BATTERIE |
|||
|
Énergie utilisable (kWh) |
41 |
||
|
Technologie |
lithium-ion |
||
|
Tension totale (V) |
400 |
||
|
Nombre de cellules |
192 |
||
|
Masse de la batterie (kg) |
305 |
||
|
MASSE DU VÉHICULE À VIDE (kg) |
1480 |
||
État de charge d’une batterie d’un véhicule électrique
Le SOC (State Of Charge) représente l’état de charge d’une batterie qui varie de 0 % (batterie « vide ») à 100 % (batterie entièrement chargée). Le SOC est directement lié à l’énergie emmagasinée par la batterie. L’énergie maximale que peut emmagasiner la batterie représente son énergie utilisable.
$SOC = \dfrac{énergie \ emmagasinée \ par \ la \ batterie}{énergie \ maximale \ que \ peut \ emmagasiner \ la \ batterie} \times 100$
Évolution du SOC (entre 0 et 80 %) en fonction du temps de charge pour la borne de recharge utilisée

Données
1,0 Wh = 3,6 x 103 J
Question 1
Calculer l’énergie massique maximale de la batterie de la voiture à partir des caractéristiques du véhicule électrique. Commenter.
Les caractéristiques de la batterie sont dans le tableau du sujet. Voici les données utiles pour cette question :
Energie utilisable = 41 kWh
Masse de la batterie = 305 kg
Pour calculer l’énergie massique, on divise l’énergie utilisable par la masse de la batterie.
Energie massique $= \dfrac{41000}{305} = 134$ Wh/kg
Cette énergie massique est bien dans l’intervalle [90 ; 180] Wh/kg ce qui est en accord avec les hypothèses énoncées dans l’introduction.
Question 2
Montrer que l’énergie emmagasinée par la batterie lors de sa charge pour passer d’un SOC de 20 % à 80 % vaut environ 25 kWh.
Grâce à la formule du SOC donnée par le sujet :
$\dfrac{énergie \ emmagasinée \ par \ la \ batterie}{énergie \ maximale \ que \ peut \ emmagasiner \ la \ batterie} \times 100$
On déduit que :
$ énergie \ emmagasinée \ par \ la \ batterie = SOC \times \dfrac{énergie \ maximale \ que \ peut \ emmagasiner \ la \ batterie}{100}$
A 20 % de charge, l’énergie emmagasinée vaut donc $20 \times \dfrac{41}{100}=8,2$ kWh
A 80 % de charge, l’énergie emmagasinée vaut donc $80 \times \dfrac{41}{100}=32,8$ kWh
La variation d’énergie entre ces deux états de charge vaut donc $32,8-8,2=24,6$ kWh.
C’est donc bien environ égal à 25 kWh.
Grâce à la formule du SOC donnée par le sujet, on peut déduire que :
$ énergie \ emmagasinée \ par \ la \ batterie = SOC \times \dfrac{énergie \ maximale \ que \ peut \ emmagasiner \ la \ batterie}{100}$
Question 3
Définir le rendement de la charge, puis le calculer. Commenter cette valeur.
Le rendement $r$ de charge peut être défini par :
$r = \dfrac{énergie \ emmagasinée \ par \ la \ batterie}{énergie \ consommée \ par \ le \ chargeur}$
Calculons l’énergie consommée par le chargeur. Pour passer de 20 % à 80 %, il faut un temps de charge $\Delta t$ de 4h d’après le graphique de charge. Or le chargeur fournit une puissance constante de 7,40 kW. L’énergie consommée par le chargeur est donc :
$E = P \times \Delta t = 7,40 \times 4 = 29,6$ kWh
$r = \dfrac{24,6}{29,6}= 83,1\%$
Question 4
On peut schématiser la conversion d’énergie du circuit de charge de la batterie lorsque le véhicule passe d’un SOC de 20 % à un SOC de 80 % de la manière suivante :
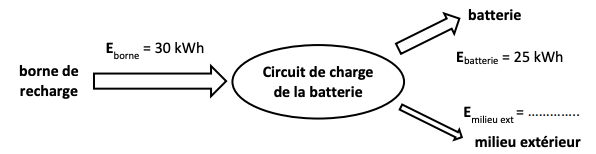
Donner la valeur manquante du schéma ci-dessus en expliquant votre démarche.
Il y a conservation de l’énergie globale au cours de la charge donc :
$E_{borne} = E_{batterie} + E_{milieu \ extérieur}$
D’où $E_{milieu \ extérieur} = E_{borne} - E_{batterie} = 5$ kWh
Question 5
L’énergie libérée vers le milieu extérieur est due à la présence d’une résistance $R_{charge}$ dans le circuit de charge.
En déduire la valeur de la résistance $R_{charge}.$ Commenter.
C’est par l’effet Joule que l’énergie est dissipée par une résistance. Cette énergie se calcule par :
$E_{milieu \ extérieur} = R_{charge} \times I^2 \times \Delta t$ où $I$ est le courant qui traverse le circuit et la durée considérée.
D’où $ R_{charge} =\dfrac{E_{milieu \ extérieur}}{I^2 \times \Delta t}$
Attention, à priori, il faut convertir l’énergie en Joule et le temps en seconde mais dans ce cas comme les deux termes sont de part et d’autre d’un quotient, on peut garder éventuellement les heures. La charge est réalisée avec un courant constant de 32 A d’après le sujet et dure 4h.
$ R_{charge} = \dfrac{10^3}{32^2 \times 4}=1, 22 \Omega$
La résistance est très faible, et c’est normal car elle correspond à la prise en compte de l’effet Joule lié aux fils électriques, soudures, etc. Malgré tout, même une petite résistance induit une chute visible du rendement.
Question 6
2. Décharge de la batterie du véhicule électrique lors de son utilisation
Le propriétaire du véhicule électrique, dont la batterie est suffisamment chargée, emprunte une autoroute horizontale et roule à vitesse constante de 100 km·h-1 pendant une durée de 5,0 minutes.
On suppose que les accessoires de la voiture (climatisation, autoradio, électronique, navigateur, etc.) consomment une puissance constante de 400 W.
Existence de frottements lorsque le véhicule roule
Lorsqu’une voiture roule à une vitesse donnée, il existe deux causes principales de dissipation de l’énergie mécanique fournie par le moteur : les frottements mécaniques en lien avec les différents mouvements associés au roulement de la voiture (parties mobiles liées à la transmission, roues, pneus, etc.) et les frottements fluides (ou aérodynamiques) liés au déplacement de l’air autour de la voiture. Les frottements fluides (ou aérodynamiques) dépendent de l’aérodynamisme de la voiture et leur action sur la voiture peut être modélisée par une force de frottement fluide (ou aérodynamique) de sens opposé à celui du vecteur vitesse de la voiture.
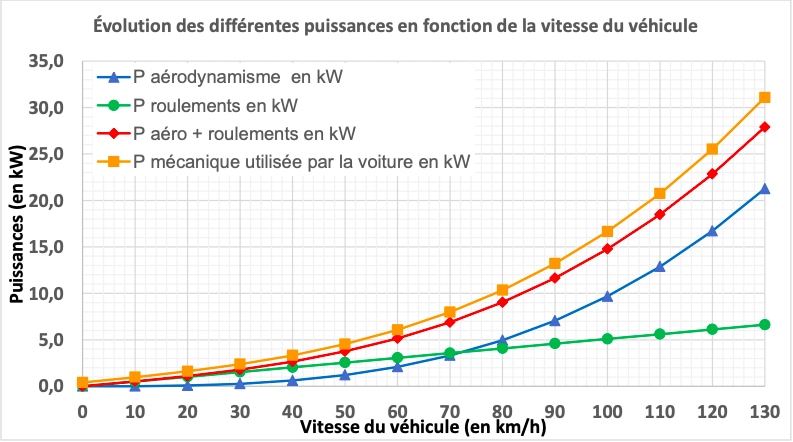
Évolution des différentes puissances en fonction de la vitesse du véhicule
Etude d’un programme de calculateur
Les voitures électriques sont généralement équipées d’un calculateur. Un exemple possible de codage d’un calculateur, lorsque la batterie possède un état de charge de 100 %, est proposé ci-dessous.

Expliquer brièvement ce que calcule ce programme.
L’utilisateur rentre la vitesse souhaitée pour son véhicule et la distance à parcourir, le programme va alors calculer si cela est bien possible.
Question 7
Modifier le programme afin de tenir compte de l’état de charge de la batterie.
La distance maximale que calcule le programme à la ligne 5 est indiquée pour 100 % de charge au départ.
Si la charge est au départ de $x %,$ il faut donc affecter à la distance maximale un coefficient multiplicateur de $\dfrac{x}{100}$ aussi.
On peut donc rajouter une ligne à la ligne 3 pour récupérer la charge initiale :
ci=float(input(« Entrez la charge initiale en pourcentage du véhicule »))
On modifie ensuite la ligne 5 par :
$d=\dfrac{ci}{100} \times (-2.913 \times v+530.2)$
La distance maximale que calcule le programme à la ligne 5 est indiquée pour 100 % de charge au départ.
Question 8
Étude mécanique du déplacement de la voiture
On s’intéresse au système {voiture} en mouvement dans le référentiel terrestre.
Comparer, à la vitesse de 100 km·h-1, les différentes puissances intervenant dans le bilan énergétique du fonctionnement de la voiture.
A 100 km/h, on peut lire sur le graphique les différentes puissances qui interviennent :
La puissance aéro+roulement, qui cumule la puissance aéro, et la puissance roulement.
La « puissance mécanique utilisée » est un peu supérieure, preuve que toutes les sources de pertes n’ont pas été prises en compte avec l’aéro et les roulements. On peut par exemple penser aux dissipations thermiques. Cette puissance « autre » représente à 100 km/h 2kW.
La puissance aéro représente 9,5 kW, la puissance roulement 5kW et la puissance électrique 400 W d’après l’énoncé.
Toutes les puissances mécaniques sont donc très largement supérieures à la puissance électrique consommée.
Question 9
Calculer la distance parcourue par la voiture pendant la durée du trajet étudié.
vitesse = 100 km/h ; durée = 5,0minutes
$d=v\times \Delta t$ où $v$ est la vitesse moyenne et $\Delta t$ la durée du trajet.
Attention, il faut convertir les km/h en m/s.
Attention, il faut convertir les minutes en secondes.
$d = \dfrac{100}{3,6} \times 5,0 \times 60 =8,3.10^3 $ m
Attention, il faut convertir les km/h en m/s et les minutes en secondes.
Question 10
Calculer l’énergie dissipée par les frottements fluides (ou aérodynamiques) pendant la durée du trajet étudié. En utilisant la notion de travail, déduire, à cette vitesse, la valeur de l’intensité de la force modélisant les frottements fluides (ou aérodynamiques). Commenter.
A 100 km/h, la puissance des frottements fluide vaut 9,5 kW d’après le graphique. Soit $E$ consommée par la voiture à cause des frottements de l’air et $P$ la puissance consommée à cause des frottements de l’air. En notant la durée de l’expérience, on a :
$E = P \times \Delta t = 9500 \times 5 \times 60 = 2,85 \times 10^6$ J
Cette énergie $E$ est égale à la valeur absolue du travail $W$ des forces de frottements fluides le long du parcours. En considérant cette force constante et opposée à la vitesse, la valeur absolue de son travail $W$ vaut $W= F \times d$ avec $F$ la force de frottement fluide et $d$ la distance parcourue.
D’où $F= \dfrac{w}{d}= \dfrac{2,85.10^6}{8,3.10^3}=3,4.10^2$ N
Cette force est équivalente au poids d’une masse de 34 kg environ. C’est une force raisonnable, grâce au travail fait sur le profil d’une voiture pour améliorer l’aérodynamisme.
