L'énoncé
Transportées par les globules rouges, les molécules d’hémoglobine assurent, par la circulation sanguine, l’apport du dioxygène aux différents organes des animaux vertébrés.
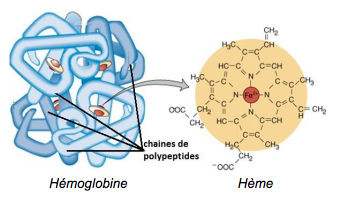
L’hémoglobine est un assemblage de quatre sous-unités qui abritent chacune une structure chimique particulière nommée hème. Chaque hème contient un ion ferreux Fe2+. Cet ion ferreux Fe2+ est responsable de la fixation d’une molécule de dioxygène.
Certains polluants ou toxines présents dans le sang peuvent oxyder les ions ferreux Fe2+ en ions ferriques Fe3+ qui n’ont pas la capacité de fixer le dioxygène. Il est donc important que l’élément fer de l’hème ne soit pas oxydé et reste sous la forme d’ion Fe2+.
Dans cet exercice, on étudie d’abord l’oxydation des ions ferreux en ions ferriques. Ensuite, une méthode de dosage de l’hémoglobine dans le sang et le traitement d’une carence en fer sont abordés.
1. Oxydation des ions ferreux
Une expérience est menée en laboratoire pour illustrer la capacité de l’ion permanganate à oxyder les ions ferreux. Dans un bécher contenant 40 mL d’une solution de sulfate de fer(II) (Fe2+(aq) + SO42- (aq)) de concentration en quantité de matière égale à 2,5 x 10-1 mol·L-1 , on introduit 20 mL d’une solution aqueuse de permanganate de potassium (K+ (aq) + MnO4- (aq)) de concentration en quantité de matière 1,0 x 10-1 mol·L-1 contenant aussi des ions H+. Les solutions avant mélange et après le mélange ont été photographiées et figurent ci-dessous.

Données :
La présence des espèces chimiques citées dans le tableau ci-dessous confère une coloration à une solution aqueuse.
| Espèce chimique | Fe2+ | Fe3+ | MnO4- | Mn2+ |
| Coloration de la solution aqueuse | Verdâtre | Orangée |
Violacée coloration intense |
Incolore |
Couples oxydant/réducteur :
- Fe3+(aq)/Fe2+(aq) ;
- MnO4-(aq)/Mn2+(aq) dont la demi-équation électronique s’écrit :
MnO4- (aq) + 8 H+ (aq) + 5 e− = Mn2+(aq) + 4 H2O(ℓ)
Question 1
À l’aide des observations, montrer qu’une transformation chimique a bien eu lieu.
On mélange une solution violette et une solution verte et on obtient une solution orange. Ce changement de couleur est caractéristique des transformations chimiques.
Lors d’une transformation chimique on peut observer un changement de couleur, l’apparition d’un solide, l’apparition d’un gaz, une augmentation de température, etc.
Question 2
Identifier les oxydants et les réducteurs consommés et ceux qui sont produits.
La solution violette contient l’ion permanganate MnO4-, les ions responsables de cette couleur. Il s’agit de l’oxydant du couple MnO4-(aq)/Mn2+(aq).
La solution verte contient les ions Fe2+, à l’origine de cette couleur. Fe2+ (aq) est le réducteur du couple Fe3+ (aq)/ Fe2+ (aq).
La couleur orange provient des ions Fe3+ (aq), oxydants qui sont produits. Les ions Mn2+, incolores, et réducteur du couple sont produits.
Donc pour résumer :
MnO4-(aq) : oxydant consommé
Mn2+(aq) : réducteur produit
Fe3+ (aq) : oxydant produit
Fe2+ (aq) : réducteur consommé
Les couples oxydant-réducteur sont écrits : oxydant/réducteur.
Question 3
On souhaite modéliser la transformation par une réaction oxydant-réducteur.
Écrire la demi-équation électronique du couple Fe3+(aq)/Fe2+(aq).
Fe3+ (aq) +1e- = Fe2+ (aq)
Question 4
Vérifier que l’équation de la réaction oxydant-réducteur modélisant la transformation chimique s’écrit : MnO4- (aq) + 5 Fe2+(aq) + 8 H+ (aq) → Mn2+(aq) + 5 Fe3+(aq)+ 4 H2O (ℓ).
La demi-équation d’oxydoréduction du couple MnO4-(aq)/Mn2+(aq) est donnée : MnO4-(aq) + 8 H+(aq) + 5 e− = Mn2+(aq) + 4 H2O(ℓ)
On écrit les deux demi-équations concernées en mettant à gauche les espèces qui réagissent donc MnO4-(aq) et Fe2+ (aq) :
(1) MnO4-(aq) + 8 H+(aq) + 5 e− = Mn2+(aq) + 4 H2O(ℓ)
(2) Fe2+ (aq) = Fe3+ (aq) +1e-
Il faut que le nombre d’électrons dans les deux demi-équations soit le même. Donc on multiplie l’équation (2) par 5 et on additionne les deux demi-équations.
MnO4-(aq) + 8 H+(aq) + 5 e− +5Fe2+ (aq)→ 5Fe3+ (aq) +5e-+ Mn2+(aq) + 4 H2O(ℓ)
En supprimant les électrons de part et d’autre de la flèche, on obtient donc bien l’équation :
MnO4-(aq) + 8 H+(aq) +5Fe2+ (aq)→ 5Fe3+ (aq) +Mn2+(aq) + 4 H2O(ℓ)
Question 5
Justifier, à l’aide des données, que MnO4- (aq) et Fe2+(aq) sont introduits en proportions stœchiométriques dans le mélange initial.
Enoncé :
Dans un bécher contenant 40 mL=V’ d’une solution de sulfate de fer(II)de concentration en quantité de matière égale à 2,5 x 10-1 mol·L-1=C’, on introduit 20 mL=V d’une solution aqueuse de permanganate de potassium de concentration en quantité de matière 1,0x 10-1 mol·L-1=C contenant aussi des ions H+. Les solutions avant mélange et après le mélange ont été photographiées et figurent ci-dessous.
Calcul de la quantité de matière initiale en MnO4- :
ni(MnO4-) = C x V = 20 x 10-3 x 1,0 x 10-1 = 2,0 x 10-3 mol
Calcul de la quantité de matière initiale en Fe2+:
ni(Fe2+) = C’ x V’ = 40 x 10-3 x 2,5 x 10-1 = 10 x 10-3 mol
ni(Fe2+)/5 = (10 x10-3)/5 = 2,0 x 10-3 mol
On a bien ni(MnO4-)/1 = ni(Fe2+)/5
Les réactifs sont placés en proportions stœchiométriques.
De manière générale, quand on a une équation de réaction aA+bB → cC+dD, si les réactifs sont en proportions stœchiométriques, on a ni(A)/a =ni(B)/b.
Question 6
Cette modélisation de la transformation sert de support pour rédiger un programme en langage python. Ce programme permet de visualiser l’évolution des quantités de matière des ions permanganate et des ions ferreux dans le système précédent en fonction de l’avancement de la réaction noté $x.$
Extrait du programme rédigé en langage python :

Représentations graphiques de l’évolution des quantités de matière calculées par le programme :
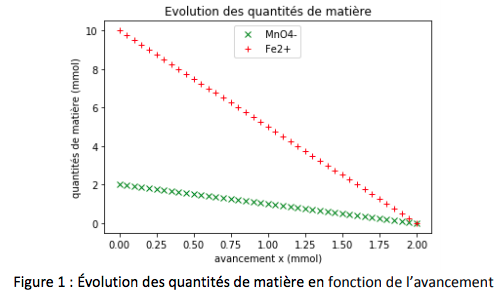
Indiquer la ligne du programme codant l’information correspondant à une transformation totale. Justifier.
Il s’agit de la ligne 20 du programme. Dans cette ligne on précise que la quantité de matière d’un des réactifs peut s’annuler : « >= 0 » donc que la transformation est totale car une transformation totale se stoppe avec la disparition d’au moins un des réactifs.
Question 7
Établir un tableau d’avancement de la réaction et vérifier que la valeur de l’avancement maximal est compatible avec le tracé de la figure 1
|
Equation |
MnO4-(aq) |
+ 8 H+(aq) |
+5Fe2+ (aq) |
→ |
5Fe3+ (aq) |
+Mn2+(aq) |
+ 4 H2O(ℓ) |
|
|
EI |
x=0 |
2,0x10-3 |
excès |
10x10-3 |
|
0 |
0 |
excès |
|
En cours |
x |
2,0x10-3-x |
excès |
10x10-3-5x |
|
5x |
x |
excès |
|
EF |
xmax |
2,0x10-3-xmax |
excès |
10x10-3-5 xmax |
|
5 xmax |
xmax |
excès |
Les réactifs sont placés en proportions stœchiométriques donc à la fin de la transformation :
nf(MnO4-)= nf(Fe2+)=0
Prenons par exemple nf(MnO4-) = 0 donc 2,0 x 10-3 - xmax = 0 et xmax = 2,0 x 10-3 mol = 2,0 mmol.
Remarque : cela revient au même avec Fe2+ : nf(Fe2+ )= 0 donc 10 x 10-3 - 5xmax = 0 et xmax =10 x 10-3/5 = 2,0 mmol.
C’est bien cette valeur que l’on lit sur le graphique : les quantités de matière en Fe2+ et en MnO4- s’annulent pour x = 2,0 mmol (schéma ci-dessous).

L’eau (le solvant) est quasiment tout le temps en excès dans ce type d’exercices. Les H+ aussi, on a d’ailleurs aucune information sur leur quantité.
Question 8
Déduire du tableau d’avancement l’expression de la quantité de matière des ions Fe3+(aq) en fonction de l’avancement.
Dans la colonne de Fe3+ du tableau d’avancement on lit : nf(Fe3+)= 5 xmax
Question 9
Écrire l’instruction permettant de calculer la quantité de matière de Fe3+(aq) pour une valeur d’avancement $x$ et proposer un numéro de ligne où elle pourrait être insérée dans le programme.
Donc : n_Ferrique.append((ni_Ferrique+5*x))
Cette ligne peut être rajoutée entre la 24 et la 25.
Pour l’instruction, on prend exemple sur la ligne 24 car c’est le même principe, on note les ions Fe3+ : « Ferrique » car c’est comme cela qu’ils sont indiqués dans le début du programme.
Question 10
Reproduire la figure 1 sur votre copie et tracer la représentation graphique de l’évolution de la quantité de matière d’ions Mn2+(aq) et celle de la quantité de matière d’ions Fe3+(aq).
Au début de la transformation ni(Mn2+) = 0 mol et ni(Fe3+) = 0 mol
A la fin de la transformation :
nf (Mn2+)= xmax= 2,0 mmol
nf(Fe3+)= 5 xmax =5 x 2,0 mmol =10 mmol
Donc pour Mn2+ on a une droite croissante qui part de (0 ;0) et finit à (2,0 ;2,0).
Et pour Fe3+on a une droite croissante qui part de (0 ;0) et finit à (10 ; 2,0).

