Fiche de cours
Fonctions cosinus et sinus - Parité, périodicité - Dérivées et représentation graphique
I) Fonctions cosinus et sinus
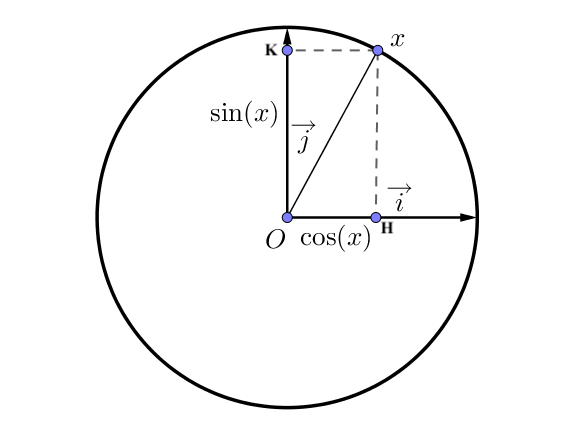
Dans le plan muni d'un repère orthonormé $(O, \overrightarrow{i}, \overrightarrow{j})$ et orienté dans le sens direct (le sens anti-horaire), on considère!re un cercle trigonométrique de centre $O$.
Pour tout réel $x$, considérons le point $N$ de la droite orientée des réels d'abscisse $x$.
A ce point, on fait correspondre un unique point $M$ sur le cercle trigonométrique par enroulement de la droite des réels sur ce cercle.
On appelle $H$ le point d'intersection entre la droite perpendiculaire à l'axe des abscisses passant par $M$ et l'axe des abscisses.
On appelle $K$ le point d'intersection entre la droite perpendiculaire à l'axe des ordonnées passant par $M$ et l'axe des ordonnées.
Définition :
Pour tout nombre réel $x$, on définit :
- la fonction cosinus et on note $x \mapsto \cos(x)$ o&ugrav
