Fiche de cours
Exercice : Modéliser une situation par une décroissance exponentielle
ÉNONCÉ
Un élément est radioactif si la structure de ses atomes est instable.
Une période est la durée nécessaire pour que la moitié des atomes de l’élément se soit transformé en un élément stable.
Un être vivant contient un équilibre constant entre le carbone 14 et le carbone 12.
La période du carbone 14 est d’environ 5730 ans.
Un échantillon contient initialement 1g de carbone 14.
QUESTIONS
1. Combien de carbone 14 restera-t-il au bout d’une période ? de deux ? de trois ?
2. Ci-dessous on a représenté la suite $\dfrac{1}{2^n}_{n \in N}.$ On l’ajuste par la fonction $f$ définie sur $\mathbb{R}^+$ par $f(t)=e^{-0,6931t}.$
Calculer l’image de $f$ par 0 ; 2 et 3,2. Interpréter.
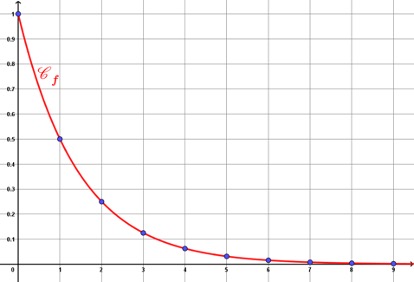
3. Pour tout $t \geq 0,$ calculer $\dfrac{f(t+1)}{f(t)}.$ Interpréter.
4. À l’aide de la fonction $f,$ déterminer au bout de combien de temps il restera moins de 0,01 g de carbone 14 dans l’éc
