Cours Inégalité triangulaire
lesbonsprofs.com
Image
Cours Inégalité triangulaire
1
Video Inégalité triangulaire
2
Exercice QCM - Inégalité triangulaire
3
Exercice Exercice - Inégalité Triangulaire
QCM
  • 1
  • 2
  • 3
  • 4
  • 5

L'énoncé

Cocher la ou les bonnes réponses

c6cb5c6b1807b64998833f4f0c04e1b27a94730b.jpg

Tu as obtenu le score de

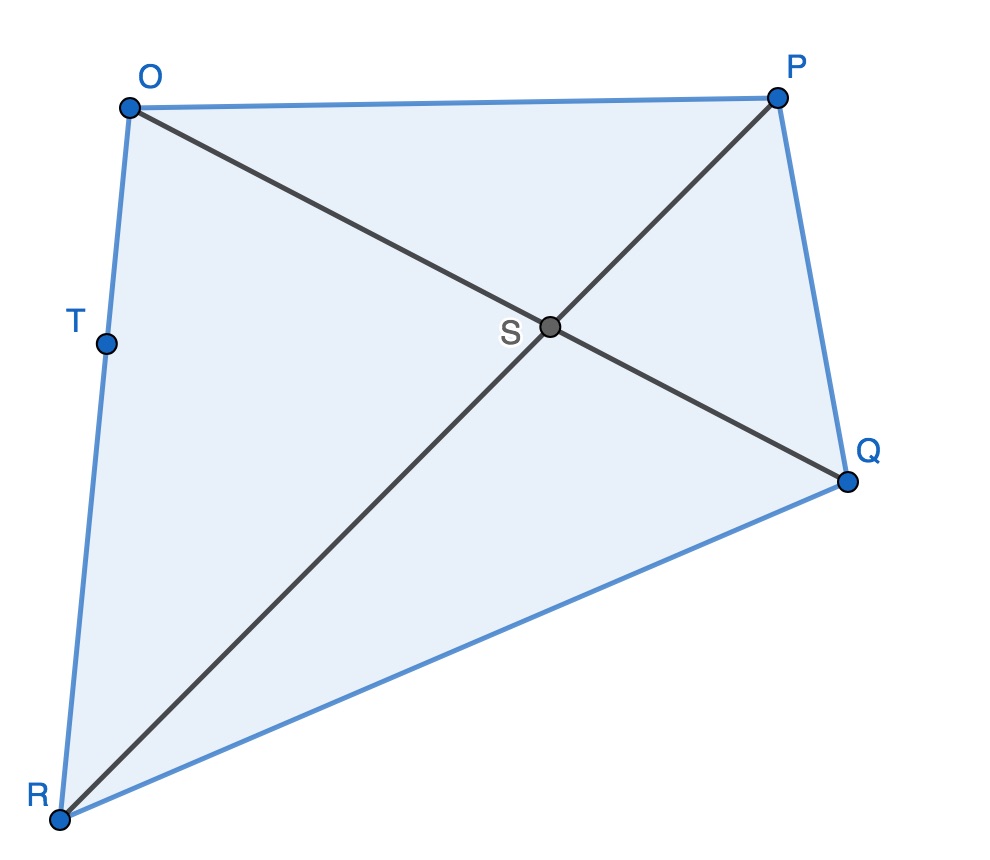
Question 1

Dans le triangle $OPS$,

c6cb5c6b1807b64998833f4f0c04e1b27a94730b.jpg

$OP<PS+SO$

$OP=PS+SO$

$OP>PS+SO$

Penser à la propriété de l'inégalité triangulaire.

Dans un triangle la longueur de chaque côté est inférieure à la somme des longueurs des deux autres côtés.
C'est une propriété du triangle elle s'applique donc au triangle $OPS$. Donc $OP<PS+SO$.

 

Question 2

Dans le triangle QSR,

c6cb5c6b1807b64998833f4f0c04e1b27a94730b.jpg

$QS=SR+RQ$

$SR=QS+QR$

$QS<SR+RQ$

$QSR=SR+RQ+QS$

Penser à l'inégalité triangulaire

Dans un triangle la longueur de chaque côté est inférieure à la somme des longueurs des deux autres côtés.
C'est une propriété du triangle elle s'applique donc au triangle $QSR$. Donc $QS<SR+RQ$.

Question 3

$PSQ$ est isocèle en $S$, on en déduit que :

c6cb5c6b1807b64998833f4f0c04e1b27a94730b.jpg

$PS=PQ$

$PS=SQ$

$PQ<PS+SQ$

$PQ<2\times{PS}$

Le triangle est isocèle en $S$ donc $PS=SQ$

Dans un triangle la longueur de chaque côté est inférieure à la somme des longueurs des deux autres côtés.
C'est une propriété du triangle elle s'applique donc au triangle $PSQ$.
Donc $PQ<PS+SQ$. Or, le triangle est isocèle en $S$ donc $PS=SQ$ donc on peut en déduire que
 $PQ<2\times{PS}$ (parce que PQ<PS+PS)

 

Question 4

Dans le triangle $OSR$,

c6cb5c6b1807b64998833f4f0c04e1b27a94730b.jpg

$OS=SR$

$OS=SR+RO$

$OS>SR+RO$

$OS<SR+RO$

Penser à l'inégalité triangulaire

Dans un triangle la longueur de chaque côté est inférieure à la somme des longueurs des deux autres côtés.
C'est une propriété du triangle elle s'applique donc au triangle $OSR$. Donc $OS<SR+RO$. 

Question 5

Toujours dans le triangle $OSR$,

c6cb5c6b1807b64998833f4f0c04e1b27a94730b.jpg

$OR=OT+TR$

$OT<TR+TO$

$OS<SR+OT+TR$

Dans un triangle la longueur de chaque côté est inférieure à la somme des longueurs des deux autres côtés.
C'est une propriété du triangle elle s'applique donc au triangle $OSR$. Donc $OS<SR+RO$.
De plus $O,T$ et $R$ sont alignés donc d'après l'autre propriété $RO=OT+TR$ par conséquent on peut écrire $OS<SR+OT+TR$.