L'énoncé
Répondre à ces questions de cours.
Question 1
Parmi ces figures, lesquelles sont des parallélogrammes ? Justifier les réponses.

1) $(AB)//(DC)$ et $(AD)//(BC)$ donc $ABCD$ est un parallélogramme.
2) $(EF)$ et $(GH)$ ne sont pas parallèles donc $EFGH$ n’est pas un parallélogramme.
3) $IJK$ ne possède que trois côtés donc $IJK$ n’est pas un parallélogramme.
4) $(LM) // (ON)$ et $(LO) // (MN)$ donc $LMNO$ est un parallélogramme.
5) $(PS) // (QR)$ et $(PR) // (QS)$ donc $PSQR$ est un parallélogramme.
6) $(WT)$ et $(VU)$ ne sont pas parallèles donc $UVWT$ n’est pas un parallélogramme.
7) $(AD) // (BC)$ et $(AB) // (CD)$ donc $ABCD$ est un parallélogramme.
8) $(EF)$ et $(GH)$ ne sont pas parallèles donc $EHGF$ n’est pas un parallélogramme.
9) $(IJ) // (KL)$ et $(IL) // (JK)$ donc $IJKL$ est un parallélogramme.
Question 2
Vocabulaire. Compléter ces phrases (avec des termes comme consécutifs, opposés, sommets, angles, diagonales...) qui décrivent le parallélogramme $ABCD$ ci-dessous :
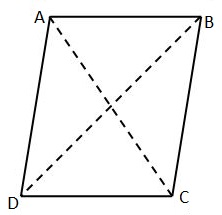
$[AB]$ et $[BC]$ sont des ?
$[AB]$ et $[CD]$ sont des ?
$A$ et $B$ sont des ?
$B$ et $D$ sont des ?
$ABC$ et $BCD$ sont des ?
$BCD$ et $BAD$ sont des ?
$[AC]$ et $[BD]$ sont les ?
$[AB]$ et $[BC]$ sont des côtés consécutifs.
$[AB]$ et $[CD]$ sont des côtés opposés.
$A$ et $B$ sont des sommets consécutifs.
$B$ et $D$ sont des sommets opposés.
$ABC$ et $BCD$ sont des angles consécutifs.
$BCD$ et $BAD$ sont des angles opposés.
$[AC]$ et $[BD]$ sont les diagonales.
Question 3
Quels noms sont corrects parmi ces derniers pour le parallélogramme de la question 2 ?
$ABCD ; BDAC ; ACDB ; BADC ; BDCA ; DABC ; CBAD ; CABD ; BCDA ; ABDC ; DBAC ; ADCB ; BACD ; DACB ; CDBA ; DCBA$
$ABCD ; BCDA ; DABC ; CBAD ; BADC ; ADCB ; DCBA$
Question 4
Combien y-a-t-il de parallélogrammes sur cette figure ? Les nommer.
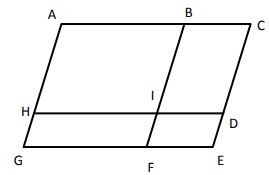
Il y en a neuf : $ACEG ; ABIH ; BCDI ; IDEF ; HIFG ; ACDH ; HDEG ; BCEF ; ABFG$
