Définition 

On appelle schéma de Bernoulli de paramètres $n$ et $p$ la répétition de $n$ expériences de Bernoulli de paramètre $p$, les répétitions étant indépendantes. 

Exemple

On lance 2 fois un dé : on répète deux fois la même expérience qui consiste à lancer le dé. 

On appelle ici succès (noté $S$ )le fait d'obtenir 1 lors d'un lancé.

Ainsi la probabilité du succès est $\dfrac{1}{6}$ et celle de l'échec $\dfrac{5}{6}$. 

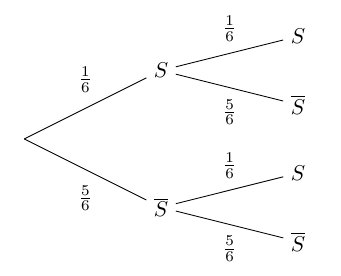
C'est donc un schéma de Bernoulli de paramètres $n = 2$ et $p = \dfrac{1}{6}$.

Un schéma de Bernoulli se représente toujours par un arbre. 

On définit à partir d'un schéma de Bernoulli une loi binomiale.

Loi binomiale 

On réalise un schéma de Bernoulli de paramètres $n$ et $p$.

On définit une variable aléatoire en posant $X$ qui compte le nombre de succès au cours des $n$ répétitions.

$X$ varie de 0 (c'est à dire 0 succès) à $n$ (c'est à dire uniquement des succès). 

La loi de probabilité de $X$ s'appelle la loi binomiale de paramètres $n$ et $p$. 

Elle est notée $\mathcal{B}(n;p)$

Exemple 

Reprenons l'exemple précédent. Il s'agit d'une loi binomiale de paramètres $n = 2$ et $p = \dfrac{1}{6}$

$X$ suit donc la loi binomiale : $\mathcal{B}(2;\dfrac{1}{6})$