Propagation et vitesse des ondes

I. Les ondes sonores

Les ondes sonores se propagent dans un milieu matériel à une vitesse $v$ : en effet les ondes sonores sont la vibration du milieu matériel (les ondes sonores ne se propagent donc pas dans le vide).

Par exemple, dans l’air à 20°C, la vitesse d’une onde sonore est de $v \simeq 340 \ m.s^{-1} $ (ou 340 m/s).

La relation fondamentale à connaître est :

$v=\dfrac{d}{t}$

où $v$ est la vitesse de l’onde (en m/s), $d$ la distance parcourue (en m) par l’onde et $t$ le temps du parcours (en s).

Exemple

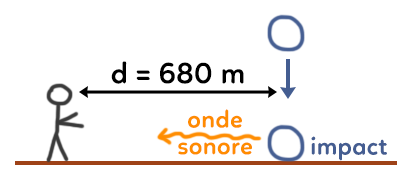
Imaginons un objet tombant sur le sol. A l’instant de l’impact, une onde sonore va être émise. La personne qui va entendre le son est à 680 m de l’impact. Combien de temps faut-il pour que l’onde sonore atteigne la personne ?

On utilise alors la relation fondamentale en isolant le temps $t$ : $t=\dfrac{d}{v}=\dfrac{680}{340}=2 \ s$

Il faut donc un certain laps de temps pour que la personne entende l'onde sonore : ce n'est pas instantané.

II. Les ondes lumineuses

Les ondes lumineuses se propagent dans le vide ou tout autre milieu transparent (en effet on reçoit bien les rayons du Soleil, alors que ceux-ci doivent traverser le vide entre la Soleil et la Terre).

La relation fondamentale se conserve mais la vitesse des ondes lumineuses est $v=3,00 \times 10^8 \ m/s$.

Cette vitesse est bien plus rapide que la vitesse des ondes sonores.