Parallélogramme - propriétés

I) Propriétés d'un parallélogramme

Si un quadrilatère est un parallélogramme, alors :

• ses côtés opposés sont parallèles (par définition)
• ses côtés opposés ont la même longueur 
• ses diagonales se coupent en leurs milieux

Exemple :

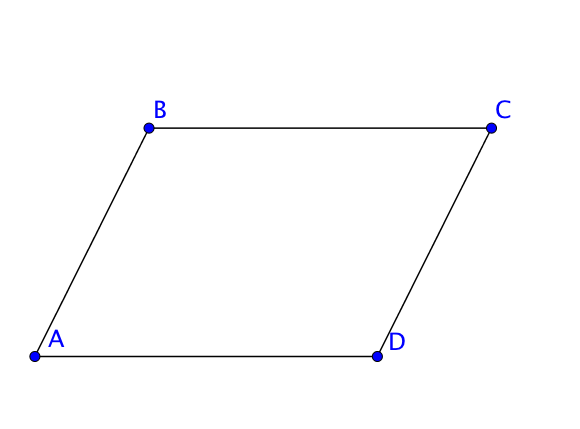
Si $ABCD$ est un parallélogramme, alors :

$(AB)//(CD)$ et $(BC)//(AD)$ car ses côtés opposés sont parallèles

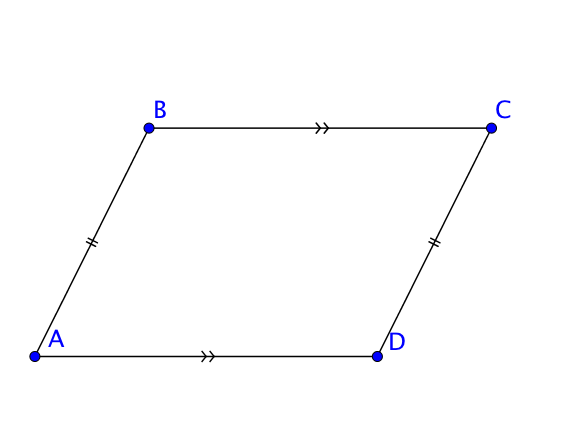
 $AD = BC$ et $AB = CD$ car ses côtés opposés ont la même longueur 

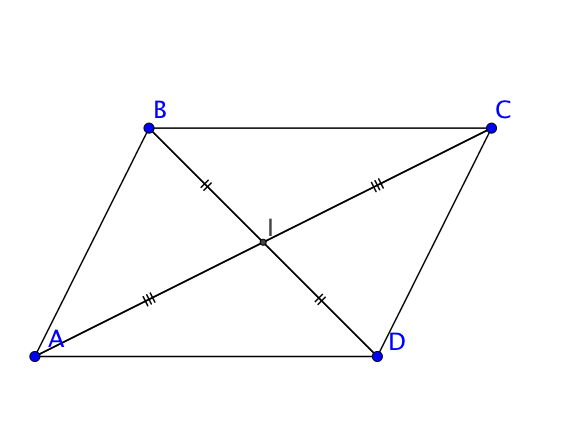
Les diagonales sont les segments $[AC]$ et $[BD]$.

Leur point d'intersection $I$ est le milieu des deux segments. Ce point est le centre de symétrie du parallélogramme.

II) Démontrer qu'un quadrilatère est un parallélogramme 

Pour démontrer qu'un quadrilatère est un parallélogramme, il s'agit de vérifier que le quadrilatère vérifie une seule des propriétés suivantes :

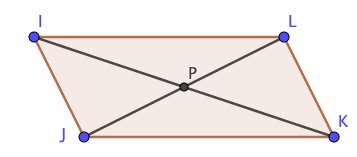
1) Les côtés opposés sont parallèles deux à deux

Exemple : si $(IJ)//(LK)$ et $(IL)//(JK)$ alors, $IJKL$ est un parallélogramme.

2) Les côtés opposés sont de même longueur deux à deux

Exemple : si $IJ = LK$ et $JK = IL$ alors $IJKL$ est un parallélogramme.

3) Deux côtés opposés sont parallèles et de même longueur

Exemple : si $IJ = LK$ et $(IJ)//(LK)$ OU $IL = JK$ et $(IL)//(JK)$ alors $IJKL$ est un parallélogramme.

4) Les diagonales se coupent en leur milieu.

Exemple : si $P$ est le point d'intersection des diagonales $[IK]$ et $[JL]$ et les coupent en leur milieu, alors $IJKL$ est un parallélogramme.

Conclusion : La propriété à utiliser dépendra donc de l'exercice et des données dont on dispose.