Les ondes progressives périodiques

I. Définition

Une onde progressive est périodique si la perturbation en un lieu donné se répète à intervalles de temps réguliers. On nomme cet intervalle la période, notée $T$. À cette période peut être associée la fréquence, par la relation suivante : $f = \dfrac{1}{T}$ avec $f$ en Hz ou en $\text{s}^{-1}$ et $T$ en s.

II. Onde progressive périodique sinusoïdale

Il s’agit d’une onde progressive périodique dont la perturbation est décrite comme une fonction sinusoïdale du temps.

Concrètement, cette perturbation représente une distance et mathématiquement, la perturbation $u(t)$ est définie par $u(t) = U_0 \times \sin( 2\pi \times f \times t \  (+ \ \phi))$, où $U_0$ est l’amplitude de la déformation et $\phi$ est la phase à l’origine et peut être omise.

La période $T$ est définie comme étant la distance entre deux maxima successifs. L’amplitude $U_0$ est la distance entre le milieu et le maximum (ou le minimum) de l’onde sinusoïdale.

III. Périodicité spatiale et temporelle

Les ondes périodiques ont une double périodicité, à la fois spatiale et temporelle.

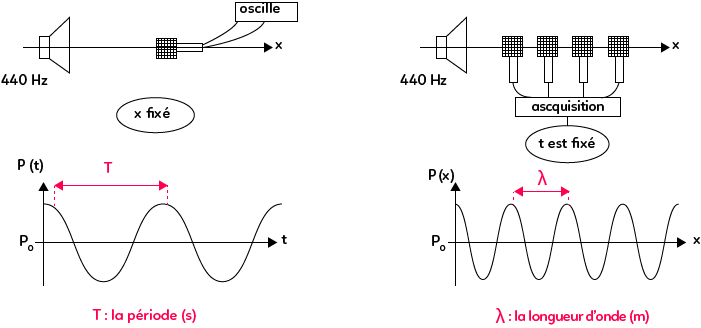
On considère deux haut-parleurs émettant un son périodique sinusoïdal (un son pur) de fréquence $f = 440 \text{ Hz}$. On place devant le premier un microphone à une distance $x$ fixée, alors que devant le second, on place plusieurs microphones à des distances différentes.

Dans le premier cas, la distance étant fixée, on mesure l’évolution de la pression en fonction du temps et on caractérise cette évolution périodique par une période temporelle $T$.

Dans le second cas, l’ensemble des microphones mesure la pression à des positions différentes et donc à un instant donné, on peut établir ce que chacun des microphones mesure. On obtient une évolution périodique, déterminée par une période spatiale $\lambda$, la longueur d’onde (en m).

Il faudra donc prêter une attention particulière à l’unité de l’axe des abscisses pour mesurer la bonne période.

Toutefois, dès lors que l’on connait une des deux périodes, on peut en déduire l’autre par la relation suivante : $\lambda = v \times T $, où $v$ est la célérité de l’onde exprimée en $\text{m.s}^{-1}$, $\lambda$ en m et $T$ en $\text{s}$.