La force gravitationnelle est une force universelle : elle s’applique partout dans l’Univers. Elle s’applique entre tous corps massiques. Entre tous corps massiques, il y a une force d’attraction. Chez soi, devant un bureau, le bureau nous attire et on attire le bureau. La Terre nous attire et c’est pour cela que l’on reste à sa surface ! Bizarrement, on attire aussi la Terre.

I. La force gravitationnelle

Pour simplifier le problème, on ne représente que deux corps : A et B.

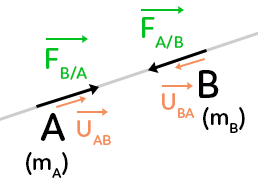
Chacun possède une masse : $m_A$ pour A et $m_B$ pour B. Ils ont une distance $AB$ entre eux. On a représenté en gris l’axe qui relie $A$ et $B.$ Les forces vont aller selon cet axe.

La force de $A$ sur $B$ est dirigée vers $A$ et se trouve le long de le ligne grise.

De même pour la force de $B$ sur $A,$ elle est dirigée vers $B.$

On a représenté deux autres vecteurs, ce sont des vecteurs unitaires. On a $\overrightarrow{u_{AB}}$ le vecteur unitaire qui se déplace de $A$ vers $B.$ C’est un vecteur donc il a une direction et un sens. Ce qui est particulier avec ce vecteur, c’est que sa norme vaut 1.

De même pour $\overrightarrow{u_{BA}}$ le vecteur de $B$ vers $A.$ Seul le sens est différent ici.

Cette force d’attraction entre $A$ et $B$ et entre $B$ et $A$ vaut : $F_{A/B} = F_{B/A}=\dfrac{G\times m_A\times m_B}{AB^2}$.

$G$ est la constante gravitationnelle donc elle a toujours la même valeur. Elle vaut 6,67.10^-11 S.I. Les masses sont en kilogramme et les distances en mètre. Attention aux conversions !

Remarque 

Puisque les forces sont opposées en sens mais leur intensité est identique, on voit que les vecteurs mesurent aussi la même taille, alors on a : $\overrightarrow{F_{A/B}}=-\overrightarrow{F_{B/A}}$.

On a aussi la relation : $\overrightarrow{F_{A/B}} = F_{A/B}\times \overrightarrow{u_{BA}}$.

Par rapport à la norme de la force, le vecteur unitaire n’apporte rien puisqu’il est égal à 1. Donc, il est présent pour dire que la force d’attraction de $A$ sur $B$ est dirigée par le vecteur unitaire $\overrightarrow{u_{BA}}$.

Comme $\overrightarrow{u_{BA}} = -\overrightarrow{u_{AB}}$, on peut remplacer dans la formule et obtenir : $\overrightarrow{F_{A/B}} = -F_{A/B}\times \overrightarrow{u_{AB}}$.

En exercice, on peut demander de calculer la force qui s’exerce entre deux corps.

II. Exemple de la Terre et de la Lune. 

La Lune subit à tout moment une force exercée par la Terre, elle tourne autour de la Terre.

On connaît quelques valeurs : la masse de la Terre $M_T$ (5,97.10²⁴ kg), la masse de la Lune $M_L$(7,34.10²² kg) et la distance entre le centre de la Terre et celui de la lune (TL = 3,8.10⁵ km). En vérité, la trajectoire n’est pas tout à fait circulaire mais un peu elliptique et donc parfois la Lune et plus proche de la Terre ou plus éloignée. La distance donnée ici est une moyenne.

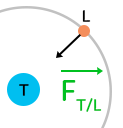
On calcule l’intensité de la force d’attraction  :

$F_{T/L} = G\times \dfrac{M_T\times M_L}{TL^2}= \dfrac{6,67.10^{-11}\times 5,97.10^{24}\times 7,34.10^{22}}{(3,8.10^5.10^3)^2}\approx 2,0.10^{20}N$.

Lorsqu’on a une sphère homogène, on va la réduire au niveau de son centre. Donc on prend toujours les distances entre les deux centres. Attention à bien mettre la distance en mètres et non en kilomètres. On multiplie par 1 000 (10³). Les points correspondent aux multiplications. Il faut aussi regarder le nombre de chiffres significatifs à indiquer dans le résultat. On prend toujours le nombre le plus petit de chiffres significatifs dans le calcul : ici c’est deux chiffres significatifs.