Déterminer les points d'intersections d'un cercle ou d'un parabole avec une droite parallèle à un axe
I) Points d'intersection d'une parabole $\mathcal{P}$ d'équation $p(x) = ax^2 + bx + c$ avec une droite $\mathcal{D}$
Remarque 1 :
Un point $M(x, y)$ appartient à la parabole $\mathcal{P}$ si et seulement si $y = p(x)$, c'est à dire que $y$ est l'image de $x$ par la fonction $p$.
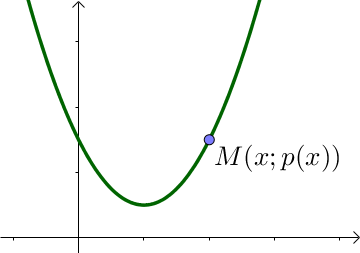
Remarque 2 :
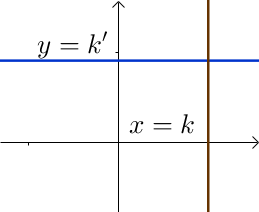
Une droite parallèle à l'axe des ordonnées a pour équation $x = k$, avec $k$ un réel.
Une droite parallèle à l'axe des abscisses a pour équation $y = k'$, avec $k'$ un réel.
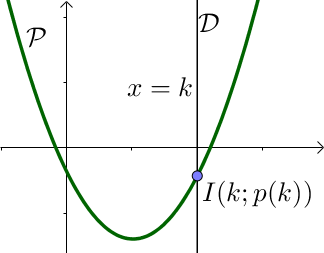
a) Droite parallèle à l'axe des ordonnées d'équation $ x= k$
Comme il ne correspond à chaque $x$ une et une seule image par la fonction $p$, il n'y a qu'un point d'intersection entre la droite et la parabole.
Ce point d'intersection appartient à la fois à la droite et à la fois à la parabole, ses coordonnées vérifient donc les équations suivantes :
$\left \{ \begin{array}{l} x = k \\ y = p(x) = ax^2 + bx + c \end{array} \right.$
Comme on sait que $x = k$, il suffit de remplacer dans la deuxième équation $x$ par $k$.
Le point d'intersection $I$ a donc pour coordonnées $I(k; p(k))$.
Exemple :
La parabole a pour équation $y = x^2 - 3x - 5$ et la droite $\mathcal{D}$ à pour équation $ x = 4$.
On calcule l'image par $p$ de $4$ : $p(4) = 4^2 - 3 \times 4 - 5 = -1$.
Ainsi, le point d'intersection $I$ à pour coordonnées $I(4; -1)$.
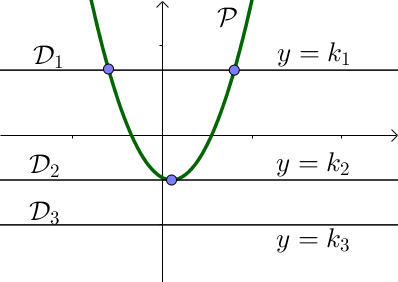
b) Droite parallèle à l'axe des abscisses d'équation $y = k$
Le nombre de solutions varie. Il peut n'y avoir aucune solution si la droite ne coupe pas la parabole ($\mathcal{D}_3$), une solution si la droite est tangente à la parabole ($\mathcal{D}_2$) ou bien deux solutions si la droite coupe la parabole($\mathcal{D}_1$) .
Les coordonnées des points d'intersection de $\mathcal{P}$ et $\mathcal{D}$ doivent vérifier
$\left \{ \begin{array}{l} y = k \\ y = p(x) = ax^2 + bx + c \end{array} \right.$
On doit alors résoudre l'équation $ax^2 + bx + c = k$.
En réécrivant l'équation sous la forme $ax^2 + bx + c - k = 0$, on se ramène à une équation du second degré que l'on résout en appliquant la méthode habituelle.
On remarque alors que le polynôme n'admet pas toujours de solutions.
Exemple :
La parabole a pour équation $y = x^2 -3x - 5$ et la droite a pour équation $y = 4$.
On doit donc résoudre l'équation $x^2 -3x - 5 = 4$ que l'on réécrit $x^2 - 3x - 9 = 0$.
Le discriminant de l'équation vaut $\Delta = 3^2 + 4 \times 9 = 45$.
On trouve alors que l'équation admet deux solutions : $x_1 = \dfrac{3 - \sqrt{45}}{2}$ et $x_2 = \dfrac{3 + \sqrt{45}}{2}$.
On trouve donc deux points d'intersections $I_1$ et $I_2$ de coordonnées : $I_1(x_1; 4)$ et $I_2 (x_2; 4)$.
II) Points d'intersection d'un cercle $\mathcal{C}$ avec une droite parallèle à un axe
Remarque :
Un point $M(x; y)$ appartient à une cercle $\mathcal{C}$ de centre $\Omega$ et de rayon $R$ si et seulement si $(x - x_{\Omega})^2 + (y - y_{\Omega})^2 = R^2$.
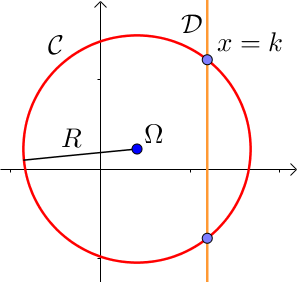
a) Droite parallèle à l'axe des ordonnées d'équation $ x= k$
La droite peut ne pas couper le cercle, être tangente en un point avec ce dernier ou le couper en deux points.
Les coordonnées des points d'intersection de $\mathcal{C}$ avec $\mathcal{D}$ vérifient
$\left \{ \begin{array}{l} x = k \\ (x - x_{\Omega})^2 + (y - y_{\Omega})^2 = R^2\end{array} \right.$
Il faut donc résoudre l'équation en $y$ : $(k - x_{\omega})^2 + (y - y_{\omega})^2 = R^2$.
On retrouve alors le fait qu'il peut y avoir 0, 1 ou 2 solutions et donc zéro, un ou deux points d'intersections entre $\mathcal{C}$ et $\mathcal{D}$.
Exemple :
On considère un cercle $\mathcal{C}$ de centre $\Omega(5; 4)$ et de rayon $R = \sqrt{8}$.
Son équation est donc $(x - 5)^2 + (y - 4)^2 = 8$. $\mathcal{D}$ a pour équation $x = 4$.
On doit alors résoudre l'équation $(4 - 5)^2 + (y - 4)^2 = 8$ que l'on réécrit sous la forme
$(-1)^2 + y^2 -8y + 16 - 8 = 0$ ce qui revient à résoudre l'équation $y^2 - 8y + 9 = 0$.
Le discriminant de cette équation vaut $\Delta = 28 > 0$.
Cette équation admet donc deux solutions $y_1 = \dfrac{8 - \sqrt{28}}{2}$ et $y_2 = \dfrac{8 + \sqrt{28}}{2}$.
Les points d'intersections sont donc $I_1(4; y_1)$ et $I_2(4; y_2)$.
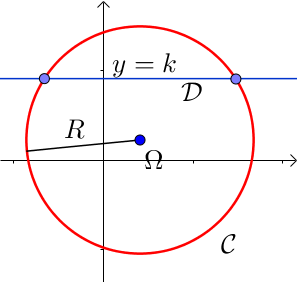
a) Droite parallèle à l'axe des ordonnées d'équation $ y= k$
La droite peut ne pas couper le cercle, être tangente en un point avec ce dernier ou le couper en deux points.
Les coordonnées des points d'intersection de $\mathcal{C}$ avec $\mathcal{D}$ vérifient :
$\left \{ \begin{array}{l} y = k \\ (x - x_{\Omega})^2 + (y - y_{\Omega})^2 = R^2\end{array} \right.$
Il faut donc résoudre l'équation en $x$ : $(x - x_{\Omega})^2 + (k - y_{\Omega})^2 = R^2$.
On retrouve alors le fait qu'il peut y avoir 0, 1 ou 2 solutions et donc zéro, un ou deux points d'intersections entre $\mathcal{C}$ et $\mathcal{D}$.
Exemple :
On considère un cercle $\mathcal{C}$ de centre $\Omega(5; 4)$ et de rayon $R = \sqrt{8}$.
Son équation est donc $(x - 5)^2 + (y - 4)^2 = 8$.
$\mathcal{D}$ a pour équation $y = 4$.
On doit alors résoudre l'équation $(x - 5)^2 + (4 - 4)^2 = 8$ que l'on réécrit sous la forme :
$ x^2 - 10y + 25 - 8 = 0$ ce qui revient à résoudre l'équation $x^2 - 10y + 17 = 0$.
Le discriminant de cette équation vaut $\Delta = 32 > 0$.
Cette équation admet donc deux solutions $x_1 = \dfrac{10 - \sqrt{32}}{2}$ et $x_2 = \dfrac{10 + \sqrt{32}}{2}$.
Les points d'intersections sont donc $I_1(x_1; 4)$ et $I_2(x_2; 4)$.


