Fiche de cours
Limite d'une fonction au voisinage de l'infini
Définitions
$\bullet$ Une fonction $f$ tend vers un réel $l$ quand $x$ tend vers $+\infty$ si, pour tout intervalle ouvert centré en $l$, il existe un réel $x_0$ tel que si $x\geqslant {x_0}$, alors $f(x)$ appartient à cet intervalle.
On notera $\displaystyle \lim_{x\to +\infty} f(x) = \ell$.
$\bullet$ Dans ce cas la droite d'équation $y=\ell$ est une asymptote horizontale à la courbe représentative de $f$ au voisinage de $+\infty$.
Ces définitions sont de même nature au voisinage de $-\infty$.
Limite au voisinage de $+\infty$
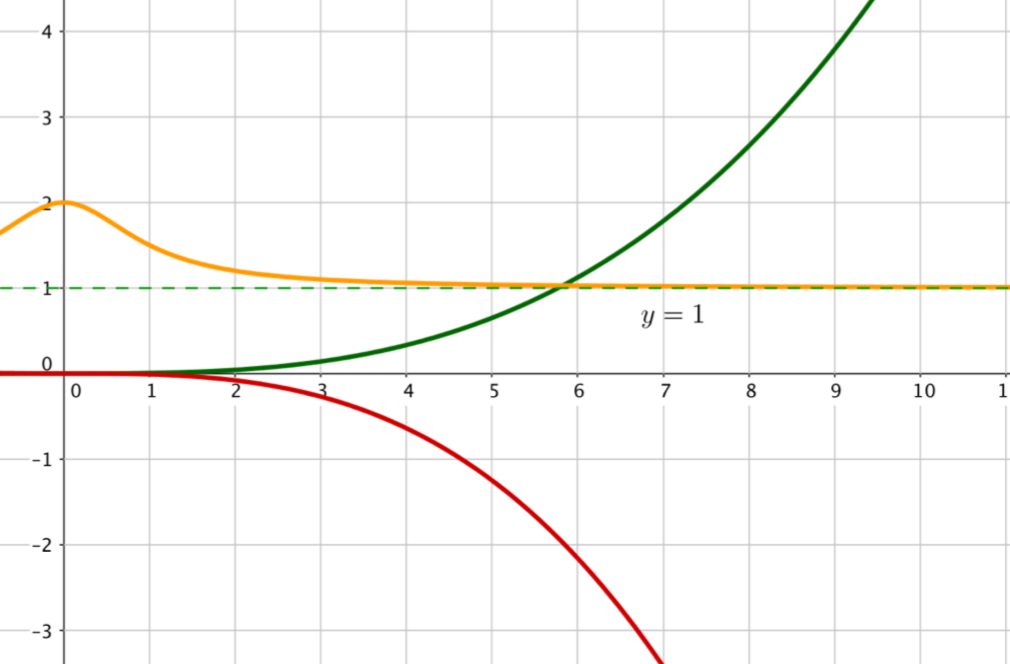
La fonction dont la courbe est en vert tend vers $+\infty$ lorsque $x$ tend vers $+\infty$.
En effet, on remarque que plus $x$ est grand, plus la valeur de $f(x)$ augmente sans que les valeurs de $f$ soient plafonnées.
La fonction dont la courbe est en rouge tend vers $-\infty$ lorsque $x$ tend vers $+\infty$.
En effet, on remarque que plus $x$ est grand, plus la valeur de $f(x)$ diminue.
La fonction dont la courbe est en orange tend vers $1$ lorsque $x$ tend vers $+\infty$.
En effet, on remarque que plus $x$ est grand, plus la val
